

 Задачи с решениями
Задачи с решениями

Из вершины острого угла ромба проведены высоты к сторонам ромба, равные 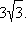 Вычислить длины диагоналей ромба.
Вычислить длины диагоналей ромба.
Пусть
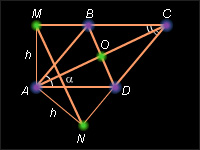 |
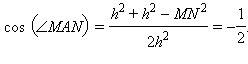 Отсюда
Отсюда
В прямоугольном треугольнике
1) ![]() MAC +
MAC + ![]() MCA = 90°
MCA = 90°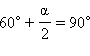 и
и
2)
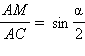 и
и
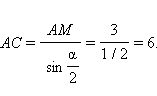 В прямоугольном треугольнике
В прямоугольном треугольнике 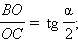
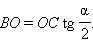 Но
Но
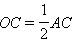 и
и
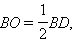 поэтому
поэтому
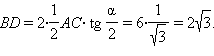
 2 из 6
2 из 6
 |