 |
 |

Свойства равнобедренного треугольника.

В равнобедренном треугольнике углы при основании равны.

В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
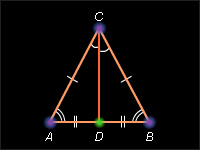
|
| Рисунок 4.3.1. Медиана, высота и биссектриса равнобедренного треугольника
|
Признаки равнобедренного треугольника.

Если в треугольнике два угла равны, то он равнобедренный.

Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.

Третий признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
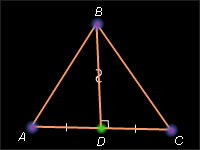
|
| Рисунок 4.3.2. К теореме 4.7
|
 |
 |
 |

