Внутри равностороннего треугольника ABC дана точка O, причем OA = 5, OB = 3, OC = 4. Найти сторону равностороннего треугольника.
Решение
Шаг 1
Построим треугольник ABC с точкой O внутри, как показано на рисунке.
Шаг 2
Осуществляем поворот на 60° относительно точки B. При этом точка A переходит в точку C, поскольку 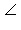ABC = 60°, точка O переходит в точку O'(BO' = BO = 3, 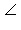OBO' = 60°). Таким образом, в результате треугольник ABO переходит в треугольник CBO'.
Шаг 3
Треугольник BOO' – равносторонний, поэтому OO' = 3. В треугольнике COO'O'C = 5, OC = 4, OO' = 3. По теореме, обратной теореме Пифагора, 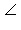O'OC = 90°.
Шаг 4
Рассмотрим треугольник OBC. В нем OB = 3, OC = 4, 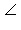COB = 90° + 60° = 150°. Из треугольника OBC по теореме косинусов имеем: BC2 = OB2 + OC2 – 2 · OB · OC · cos 150° =
Задачи с решениями
7 из 8
