 |
 |
Гомотетией с центром 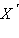 так, что
так, что
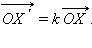 (см. рис. 12.6.1).
(см. рис. 12.6.1).
|
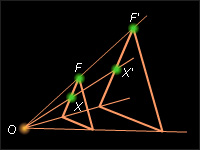
| Рисунок 12.6.1. Гомотетия
|

При гомотетии с коэффициентом

Гомотетия с коэффициентом 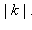

Подобие с коэффициентом

Гомотетия отрезок переводит в отрезок.

Гомотетия сохраняет величину угла.

Гомотетия треугольник переводит в треугольник. Стороны этих треугольников пропорциональны, а соответственные углы равны.

Композиция подобий с коэффициентами
 |
 |
 |

