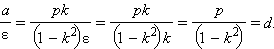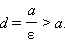Глава 10. Декартовы координаты
10.8. Эллипс и его свойства
В § 7 было получено уравнение фигуры, которую мы назвали эллипсом:
Перейдем в новую систему координат, перенеся начало системы координат в точку 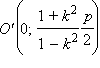 и повернув оси исходной системы на угол 90°.
и повернув оси исходной системы на угол 90°.
В соответствии с формулами преобразования координат выразим старые координаты через новые по формулам:
или
В новой системе координат, которую называют канонической, уравнение эллипса имеет вид
при этом
то есть при k < 1 получим, что a > b > 0. В дальнейшем для удобства будем опускать знак "штрих" и будем вместо x' (y') писать x (y). Таким образом, получим уравнение эллипса в новой системе координат.
Это уравнение называется каноническим уравнением эллипса.
Рассмотрим свойства эллипса.
Свойство 10.1.
Эллипс пересекает каждую из осей координат в двух точках.
Для определения точек пересечения эллипса с осью Ox нужно решить совместно два уравнения
Отсюда получим x = ±a. Таким образом, точками пересечения эллипса с осью Ox будут точки A (a; 0) и C (–a; 0).
Аналогично, точки пересечения эллипса с осью Oy – B (0; b) и D (0; –b).
|
Точки A, B, C и D называются вершинами эллипса. Отрезок AC называется большой осью эллипса, отрезок BD – малой осью. Числа a и b называют полуосями эллипса. Точки 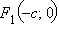 и
и 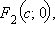 где
где 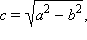 называются фокусами эллипса.
называются фокусами эллипса.
Пусть M (x; y) – произвольная точка эллипса. Найдем расстояния от точки M до фокусов эллипса.
Рассмотрим выражение
Здесь мы учли, что координаты (x; y) точки M удовлетворяют уравнению эллипса.
Величину 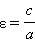 называют эксцентриситетом эллипса. Очевидно, для эллипса ε < 1. Поскольку
называют эксцентриситетом эллипса. Очевидно, для эллипса ε < 1. Поскольку 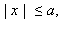 то отсюда следует, что a – εx > 0. Поэтому
то отсюда следует, что a – εx > 0. Поэтому 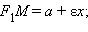
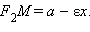
Свойство 10.2.
Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.
Действительно, используя полученные выражения для расстояний от точки эллипса до его фокусов, получим
|
Свойство 10.3.
Эллипс имеет две взаимно перпендикулярные оси симметрии.
Свойство 10.4.
Эллипс имеет центр симметрии.
Если координаты точки M (x; y) удовлетворяют уравнению эллипса, то этому же уравнению удовлетворяют и координаты точки N (–x; –y). Точка M симметрична точке N относительно начала координат. Таким образом, эллипс имеет центр симметрии.
|
Центр симметрии эллипса называется центром эллипса.
Свойство 10.5.
Эллипс может быть получен сжатием окружности.
Пусть 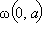 – окружность с центром в начале координат и радиуса a. Тогда – окружность с центром в начале координат и радиуса a. Тогда
Точке 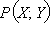 на окружности сопоставим точку 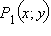 такую, что
Точка 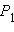 получается сдвигом точки P, при котором абцисса не меняется, а ордината уменьшается в отношении 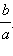
Координаты точки 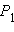
удовлетворяют уравнению эллипса. В самом деле,
Таким образом, эллипс можно получить из окружности равномерным сжатием к оси Ox, при котором ординаты точек уменьшаются в одном и том же соотношении, равном 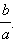 Отсюда следует, что форма эллипса зависит от значения отношения Отсюда следует, что форма эллипса зависит от значения отношения 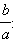 чем меньше это отношение, тем более сжатым будет эллипс, и наоборот, чем больше отношение чем меньше это отношение, тем более сжатым будет эллипс, и наоборот, чем больше отношение 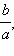 тем эллипс будет менее сжатым. тем эллипс будет менее сжатым.
|
В качестве характеристики формы эллипса удобнее пользоваться эксцентриситетом. Так как
то чем больше ε, тем более сжат эллипс.
При малых значениях эксцентриситета эллипс мало отличается от окружности. При ε = 0 эллипс превращается в окружность.
В § 7 мы определили эллипс как множество точек, отношение расстояний от которых до данной точки A и данной прямой l есть величина постоянная и равная числу k.
Рассмотрим, какие координаты имеет точка A и какое уравнение – прямая l в канонической системе координат. Для начала отметим, что в силу введенных ранее обозначений
Тогда
Таким образом, данное в условии исходной задачи число, характеризующее величину отношения расстояний от точки эллипса до точки A и прямой l, есть эксцентриситет эллипса.
Координаты точки 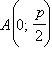 при переходе в новую систему будут равны:
при переходе в новую систему будут равны:
То есть точка A в новой системе координат имеет те же координаты, что и фокус 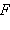 эллипса и поэтому совпадет с ним.
эллипса и поэтому совпадет с ним.
Уравнение прямой в исходной системе координат имело вид 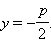 После замены системы координат получим новое уравнение прямой l
После замены системы координат получим новое уравнение прямой l
Обозначим 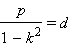 и покажем, что
и покажем, что 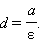 Действительно,
Действительно,
Поскольку для эллипса ε < 1, то 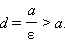
Прямая x = –d называется директрисой, соответствующей фокусу F1(-c; 0). Наряду с этой директрисой вводят прямую x = d, которая является директрисой, соответствующей фокусу F2(c; 0).
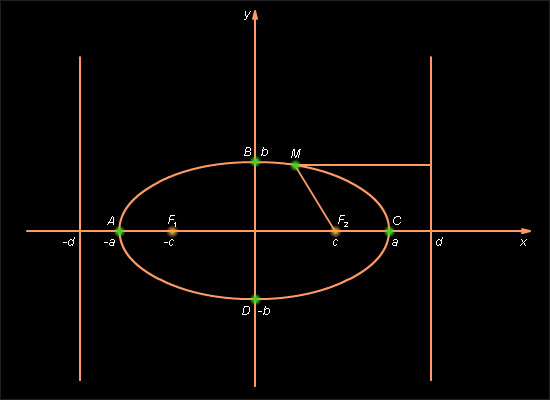
С учетом свойств симметрии эллипса, свойство, с помощью которого мы определили эллипс, в новых терминах можно сформулировать следующим образом: отношение расстояния от любой точки эллипса до одного из его фокусов к расстоянию от этой точки до соответствующей ему директрисы есть величина постоянная и равная эксцентриситету. Вид эллипса в канонической системе координат и его директрисы приведены на рис. 10.8.1.
 1
|
| Рисунок 10.8.1
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


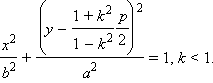
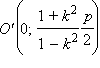 и повернув оси исходной системы на угол 90°.
и повернув оси исходной системы на угол 90°.
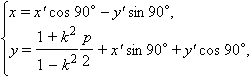
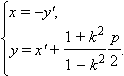
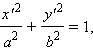
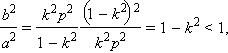
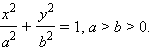
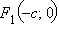 и
и 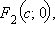 где
где 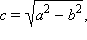 называются фокусами эллипса.
называются фокусами эллипса.
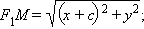
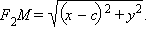
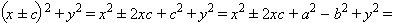
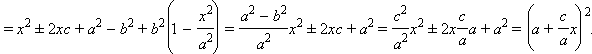
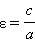 называют эксцентриситетом эллипса. Очевидно, для эллипса
называют эксцентриситетом эллипса. Очевидно, для эллипса 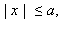 то отсюда следует, что
то отсюда следует, что 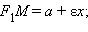
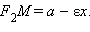
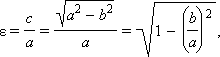
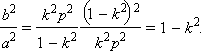
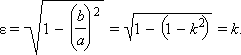
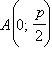 при переходе в новую систему будут равны:
при переходе в новую систему будут равны:
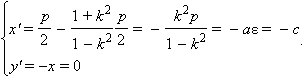
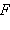 эллипса и поэтому совпадет с ним.
эллипса и поэтому совпадет с ним.
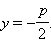 После замены системы координат получим новое уравнение прямой
После замены системы координат получим новое уравнение прямой 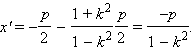
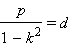 и покажем, что
и покажем, что 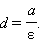 Действительно,
Действительно,