Изменим формулировку задачи предыдущего параграфа, заменив одну из точек прямой, а именно: найти множество точек, отношение расстояний от которых до данной точки и данной прямой есть величина постоянная.
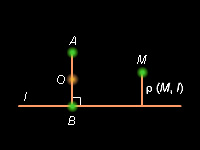
Пусть заданы прямая l и точка A, не лежащая на этой прямой, а также положительное число k. Выберем систему координат, поместив ее начало в точку O – середину перпендикуляра AB, опущенного на прямую l. Луч OA при этом примем за положительную полуось Oy (см. рис. 10.7.2)
1
Рисунок 10.7.1
Обозначим расстояние от точки M до прямой l символом Тогда, если M – некоторая точка искомого множества, то условие запишется в виде
Пусть AB = p. Тогда координаты точки A будут а прямая l однозначно задается уравнением Так как и то уравнение искомой фигуры можно записать в виде
Это уравнение равносильно
Упростив, получим
Рассмотрим различные случаи.
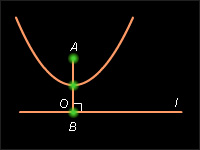
Пусть k = 1. Тогда уравнение имеет вид Известно, что это уравнение параболы. Отсюда получим, что геометрическим местом точек, равноудаленных от данной точки и данной прямой, является парабола (см. рис. 10.7.2).
2
Рисунок 10.7.2
Для дальнейшего анализа преобразуем исходное уравнение, выделив полный квадрат по переменной y:
или
Поделив на выражение, стоящее в правой части, получим
Если k < 1, введем новые обозначения: Тогда уравнение запишется в более простой форме
Если k > 1, обозначим как и раньше и получим уравнение
Фигура, полученная в случае k < 1, называется эллипсом, а в случае k > 1 – гиперболой. Свойства полученных фигур будут исследованы далее.
Тогда, если 
а прямая 
Так как 
и 
то уравнение искомой фигуры можно записать в виде
Известно, что это уравнение параболы. Отсюда получим, что геометрическим местом точек, равноудаленных от данной точки и данной прямой, является парабола (см. рис. 10.7.2).
Тогда уравнение запишется в более простой форме
и получим уравнение
