 |
 |
Программа «Графер» предназначенa для построения и преобразования графиков функций различного вида. Графер обеспечивает демонстрацию связи формулы и графика функций. Для школьников использование Графера облегчает изучение графиков функций, обеспечивает наглядность и простоту в использовании. Для преподавателей Графер может служить хорошим средством для подготовки к занятиям, для создания наглядных пособий и т. д.
Построение графиков функций можно производить в декартовой и полярной системах координат. Пользователь может самостоятельно задать функцию вида
Графер даёт возможность производить над функциями и их графиками различные преобразования: смещение графика функций относительно координатных осей, сжатие, растяжение, зеркальное отображение относительно осей координат. Можно производить взаимные преобразования нескольких функций, такие как сложение функций, умножение и деление одной функции на другую, преобразование вида
Имеются различного рода графические возможности, предназначенные для оформления графиков функций, для придания им более наглядного вида. Можно ставить надписи, отмечать точки, отрезки, интервалы и многое другое.
Так как для построения функций используются численные, а не аналитические методы, возможны некоторые неточности построения в сложных критических точках.
C помощью программы «Графер» можно создавать симуляции, демонстрирующие различные математические законы и теоремы, связанные с графиками и их функциями.
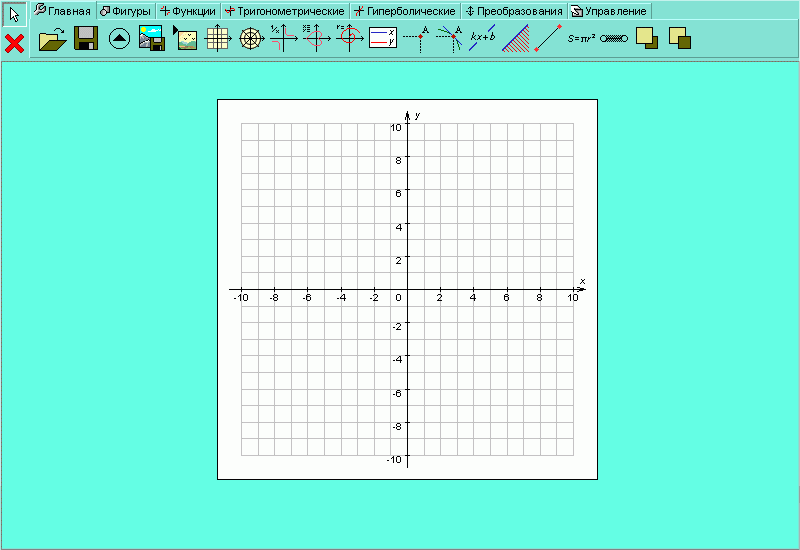
Панель инструментов имеет многофункциональную структуру. Она разделена закладками на 7 групп: , , , , , , (рисунок H.2.4.1). Наибольший интерес для широкого круга пользователей представляют первые шесть групп. Группа даёт пользователю возможности, которые позволяют сохранять данные, создавать координатные плоскости, строить графики всевозможных, задаваемых произвольным образом функций. предназначена для создания схематических рисунков и надписей. Группы , , предназначены для построения графиков стандартных функций, параметры которых пользователь может задавать самостоятельно. Группа позволяет преобразовывать функции и их графики. Группа используется для написания объектно-ориентированных программ, с целью создания симуляций, демонстрирующих различные преобразования, законы и теоремы, связанные с функциями и их графиками. При загрузке программы сразу появляется декартовая координатная плоскость, параметры которой при необходимости можно изменить (это будет рассмотрено более подробно в следующих разделах руководства).
|
| Рисунок H.2.4.1.1. Внешний вид программы «Графер»
|
Программа «Графер» даёт пользователю возможность задавать функции вида
|
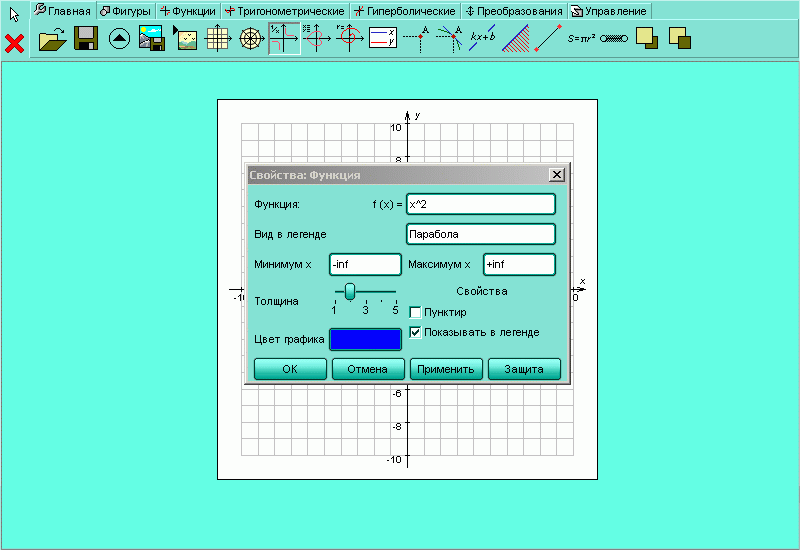
| Рисунок H.2.4.1.2. Свойства задаваемой функции
|
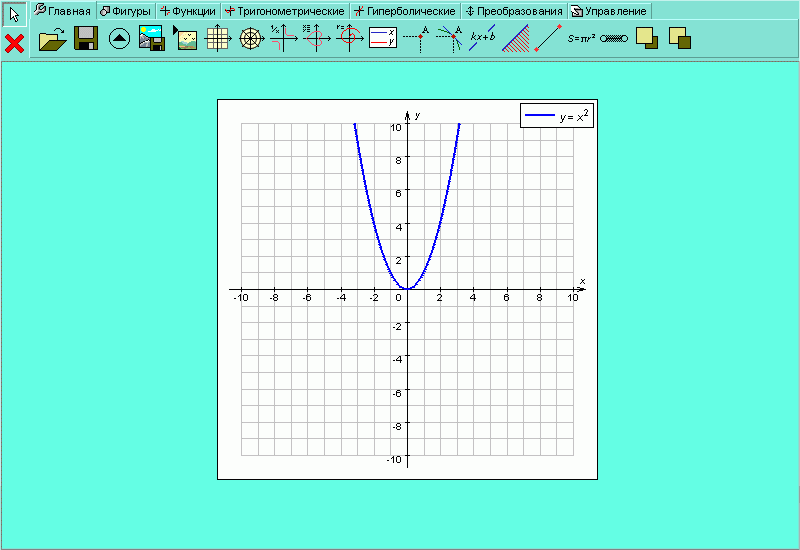
Посмотрим, как это можно делать на примере функции
|
| Рисунок H.2.4.1.3. График функции |
Как изменить параметры графика функции
Для того чтобы изменить параметры графика функции, выберите закладку , нажмите на панели инструментов кнопку , наведите курсор мыши на график функции и два раза кликните на нём левой кнопкой. Откроется окно , в котором вы можете изменить параметры графика функции.
Аналогичным образом производятся изменения параметров всех остальных объектов Графера.
Построение элементарных графиков функций
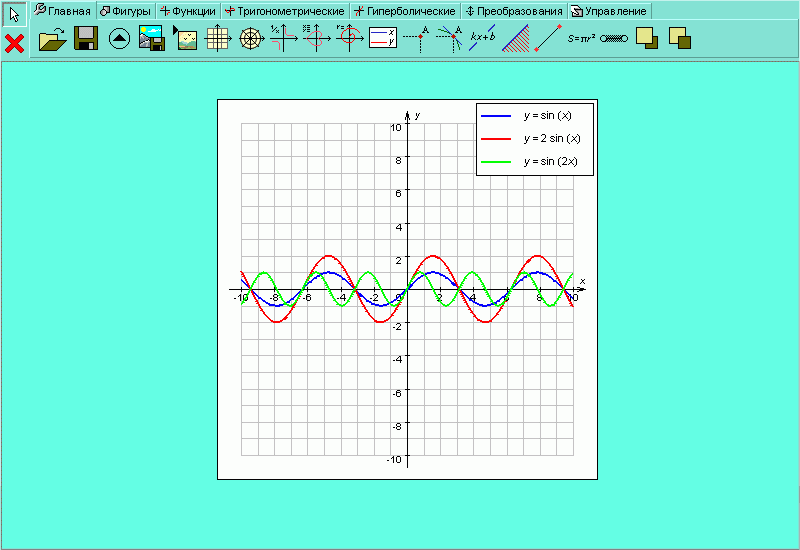
Программа «Графер» позволяет работать с элементарными функциями: степенными, тригонометрическими и гиперболическими. Для примера выберите закладку и постройте график какой-нибудь тригонометрической функции, например
|
| Рисунок H.2.4.1.4. Графики функций вида |
Как изменить масштаб координатной плоскости
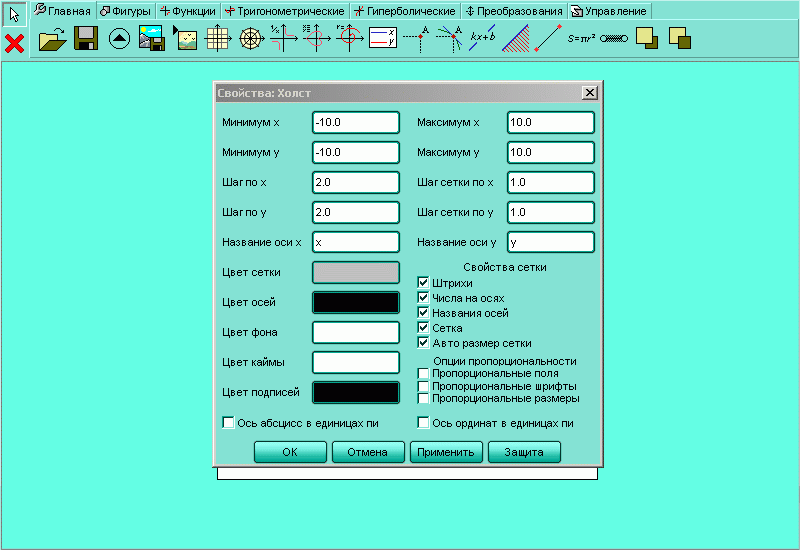
Попробуйте изменить масштаб координатной плоскости. Для этого на панели инструментов нажмите на кнопку , затем переведите курсор мыши на координатную плоскость и щёлкните один раз левой кнопкой. После этой манипуляции координатную плоскость можно подвергать различного рода трансформациям. По краям координатной плоскости появились чёрные маркеры. Наведя курсор мыши на один из маркеров, вы можете сжать или растянуть координатную плоскость в любом направлении. Для того, чтобы задать новый масштаб и внести изменения в ряд других свойств, наведите курсор мыши на координатную плоскость и щёлкните два раза левой кнопкой мыши. Откроется окно (рисунок H.2.4.5). Теперь вы можете задать границы шкалы и шаг сетки по осям, цвета фона, осей, сетки и подписей, названия осей, отображение всех этих элементов и другие свойства координатной плоскости.
|
| Рисунок H.2.4.1.5. Задание нового масштаба для координатной плоскости и изменение её свойств
|
Как удалить, сохранить данные, извлечь сохранённые данные
Если у вас возникла необходимость удалить какой-нибудь объект, воспользуйтесь кнопкой на панели инструментов. Для этого после нажатия кнопки, наведите курсор мыши на тот объект, который вы хотите удалить и щёлкните один раз левой кнопкой. Также вы можете удалить объект с помощью кнопки Delete, находящейся на клавиатуре. Для этого выделите требуемый объект при помощи кнопки , находящейся на панели инструментов, а затем нажмите на кнопку Delete, находящуюся на клавиатуре.
Если вам необходимо, чтобы Графер начал свою работу сначала и не сохранял данные, введённые вами до этого, воспользуйтесь кнопкой Панели инструментов.
Для того, чтобы сохранить введённые вами данные, выберете закладку на панели инструментов и воспользуйтесь кнопкой . График сохранится в файле с расширением *.set. Вы сможете получить доступ к сохранённым данным при помощи кнопки , находящейся по соседству с кнопкой .
Можно сохранить введённые данные в виде рисунка с расширением *.jpg при помощи кнопки .
Преобразования графиков и их функций
Выберите закладку . Давайте теперь произведём обратное преобразование какого-нибудь графика функции. Для этого нажмите на панели инструментов кнопку , наведите курсор мыши на тот график функции, который вы хотите подвергнуть преобразованию, щёлкните один раз левой кнопкой. Выбранный вами график выделится штрихпунктирной линией. После этого нажмите на панели инструментов кнопку , и вы получите обратное преобразование выделенной функции.
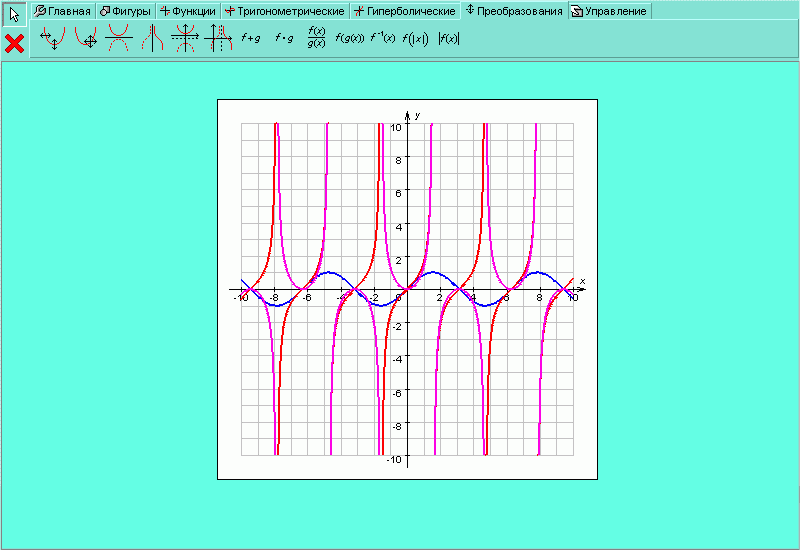
Для преобразования двух функций (например для того, чтобы перемножить две функции) вам необходимо одну из функций выделить так, как это делалось для нахождения обратной функции, а вторую функцию выделить следующим образом: держа нажатой кнопку Shift на клавиатуре и, наведя курсор мыши на график функции, щёлкнуть один раз левой кнопкой. Далее действуйте так же, как при нахождении обратной функции. На рисунке H.2.4.6 розовым цветом представлен результат преобразования
|
| Рисунок H.2.4.1.6. Результат преобразования |
С помощью можно проделать ещё ряд преобразований: переместить график в любое место координатной плоскости, сжать и растянуть, произвести различные зеркальные отображения, взять модуль.
Когда вы производите какие-нибудь преобразования графиков функций, то они влияют не только на графическое представление функции, но и на её аналитический вид. «Графер» даёт возможность наблюдать как за графическими, так и за аналитическими изменениями функции при различных преобразованиях графиков функций. Для того чтобы посмотреть на то, какой аналитический вид имеет функция после преобразования, нажмите на кнопку , находящуюся на панели инструментов, наведите курсор мыши на тот график функции, который был подвержен преобразованию, и кликните на нём два раза мышкой. В диалоговом окне вы увидите формулу функции.
Схематические надписи и рисунки
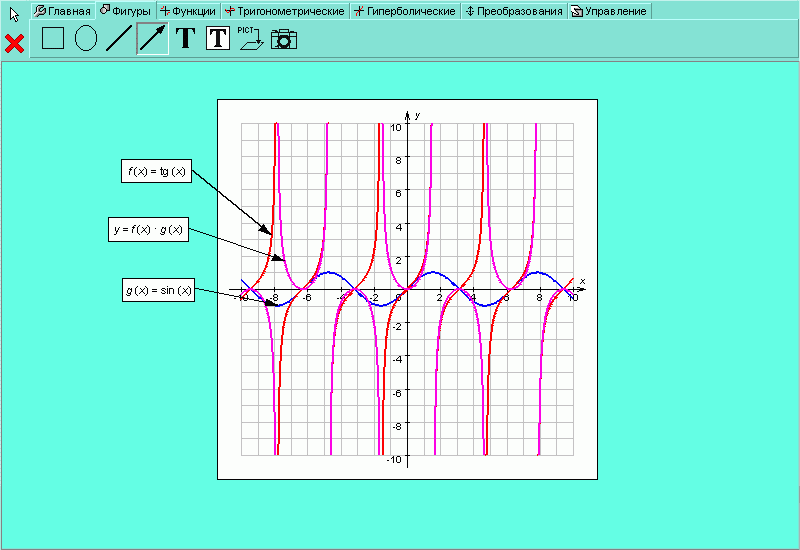
Вы можете сделать схематические надписи для большей наглядности полученной картинки. Для этого выберете закладку . Проведите к каждому из полученных в предыдущем пункте графиков стрелочки и сделайте к ним соответствующие графикам функций надписи, отражающие суть проделанных нами преобразований (рисунок H.2.4.7). Используя закладку , можно построить прямоугольник, овал и другие графические примитивы. В свойствах можно задать цвет фигуры, а также сделать её закрашенной.
|
| Рисунок H.2.4.1.7. Схематические надписи
|
Кнопка , находящаяся в группе , даёт возможность записывать различные математические выражения и формулы с использованием специальных символов и знаков, делать надписи на координатной плоскости.
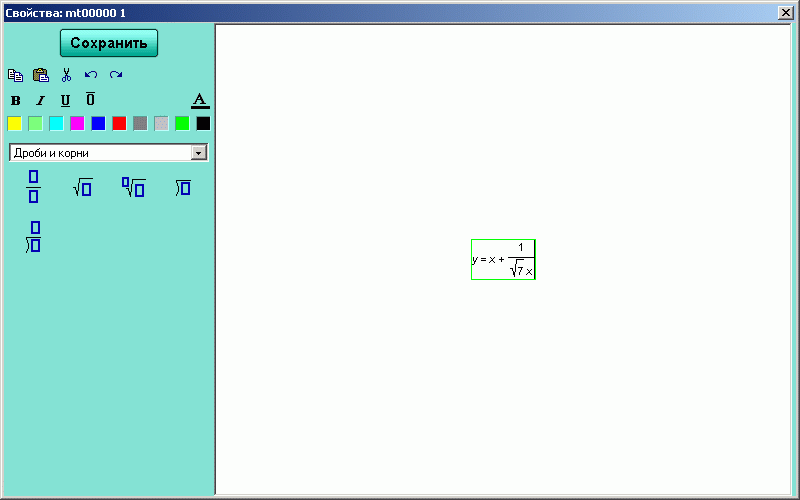
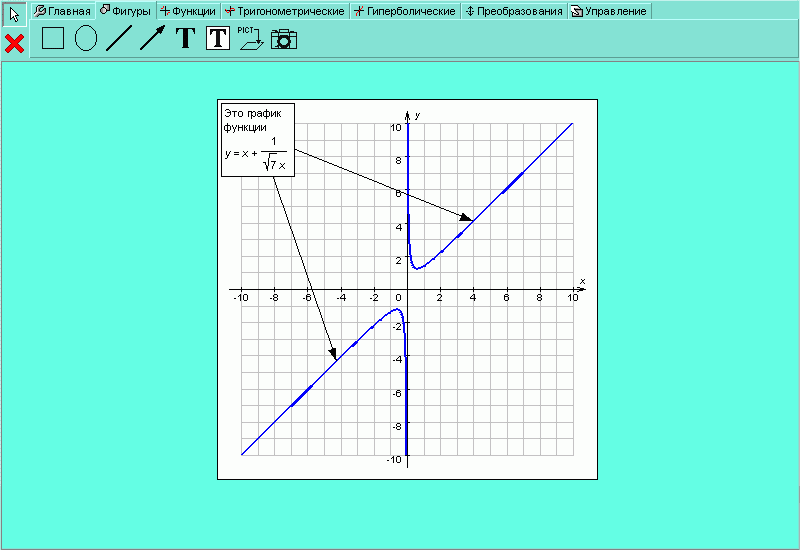
Для того чтобы воспользоваться этой возможностью, выберите закладку на панели инструментов, нажмите на кнопку , переведите курсор мыши в то место координатной плоскости, где вы хотите сделать надпись и один раз щёлкните левой кнопкой мыши. Откроется окно редактора, изображённое на рисунке H.2.4.8. Теперь произведите нужную вам надпись и, нажав на кнопку , находящуюся в окне редактора формул, вставьте эту надпись на координатной плоскости (рисунок H.2.4.9).
|
| Рисунок H.2.4.1.8. Редактор формул и математических выражений
|
|
| Рисунок H.2.4.1.9. Математическое выражение, записанное в редакторе формул и математических выражений, вставили в рисунок
|
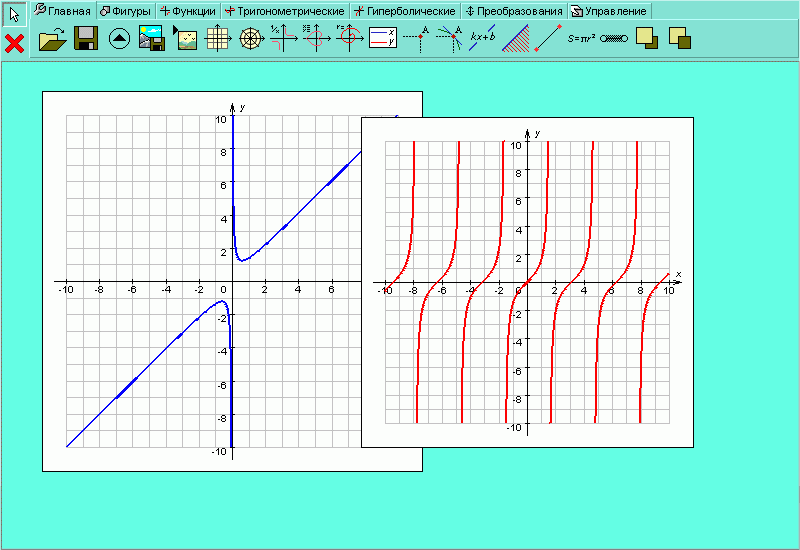
Вы можете работать одновременно с несколькими координатными плоскостями, как показано на рисунке H.2.4.10. Для того чтобы поместить одну координатную плоскость поверх другой и наоборот, выберите закладку и воспользуйтесь кнопками или .
|
| Рисунок H.2.4.1.10. Работа с несколькими координатными плоскостями
|
Группа содержит в себе функции, с помощью которых можно: выделять на графике функций точки, интервалы, рисовать отрезки, касательные, прямые и полуплоскости. Такие возможности могут понадобиться для графического решения уравнений, неравенств, систем уравнений и неравенств, а также для графического представления теорем и математических законов.
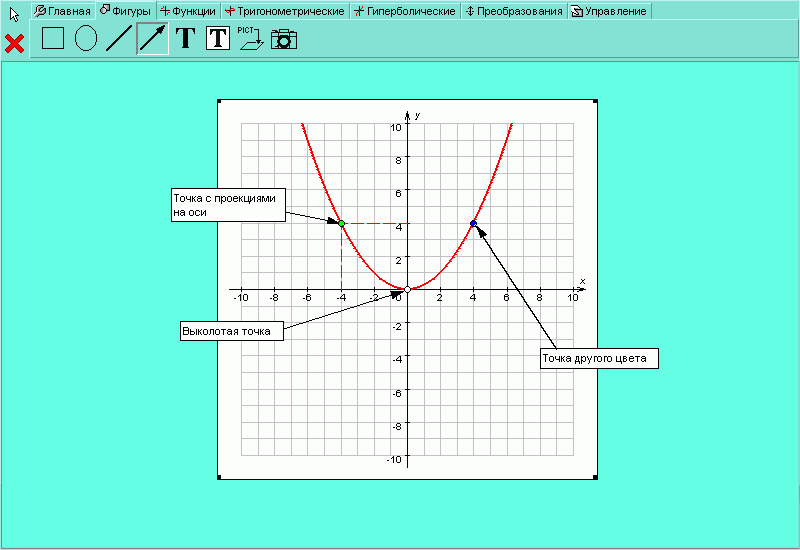
Для того чтобы выделить на графике функций какую-нибудь точку, нажмите на кнопку , наведите курсор мыши на то место графика функции, где вы хотите поставить точку, и один раз кликните левой кнопкой мыши, появится точка. При необходимости можно нарисовать выколотую точку, поменять размер точки, цвет, нарисовать точку с проекциями на оси (рисунок H.2.4.11). Все эти изменения производятся в окне .
|
| Рисунок H.2.4.1.11. Точки
|
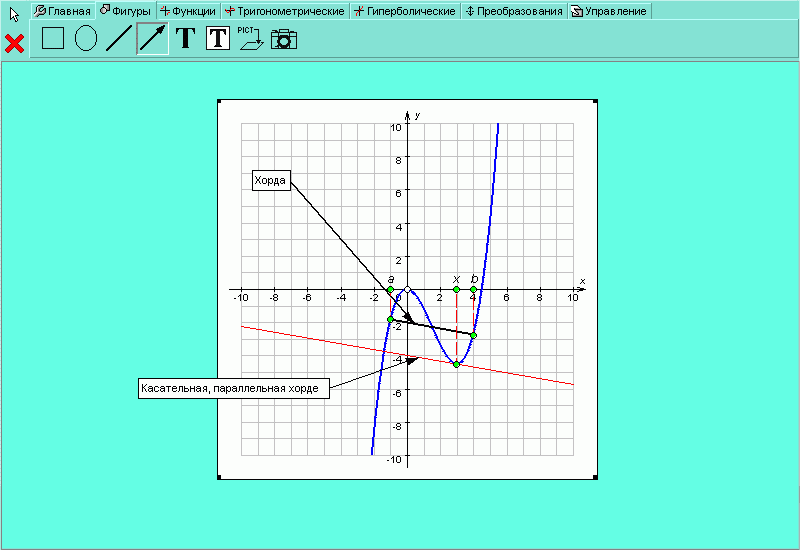
В группе есть такие кнопки, как и , которые могут понадобиться для графического представления математических теорем, например для графического представления теоремы Лагранжа (рисунок H.2.4.12).
|
| Рисунок H.2.4.1.12. Графическое представление теоремы Лагранжа
|
Кнопки и группы используют для графического решения уравнений, неравенств и систем уравнений и неравенств. Об их практическом применении будет говориться в пункте «Уравнения и неравенства».
С помощью программы «Графер» можно легко получать графические решения уравнений, систем уравнений и неравенств, это способствует хорошему пониманию при изучении уравнений, систем уравнений и неравенств. Вы можете аналитически решить задачу, а потом проверить правильность своего решения с помощью программы «Графер».
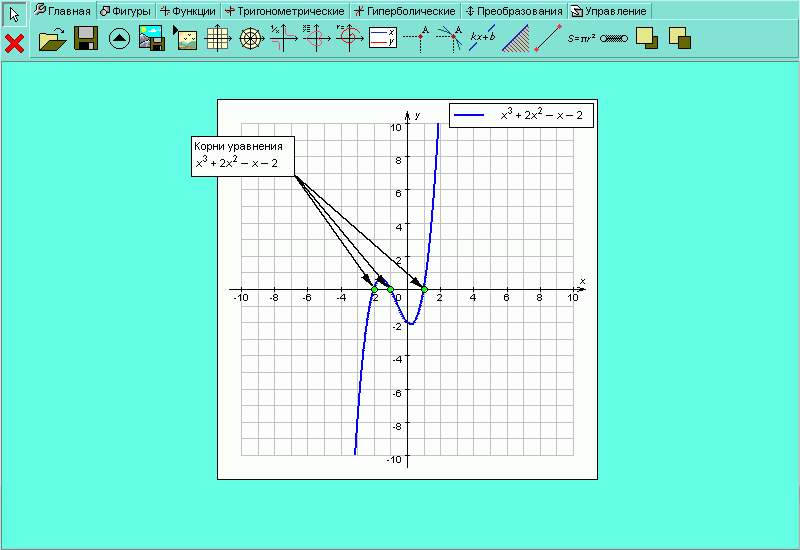
Давайте получим графическое решение уравнения
|
| Рисунок H.2.4.1.13. Графическое представление решения уравнения
|
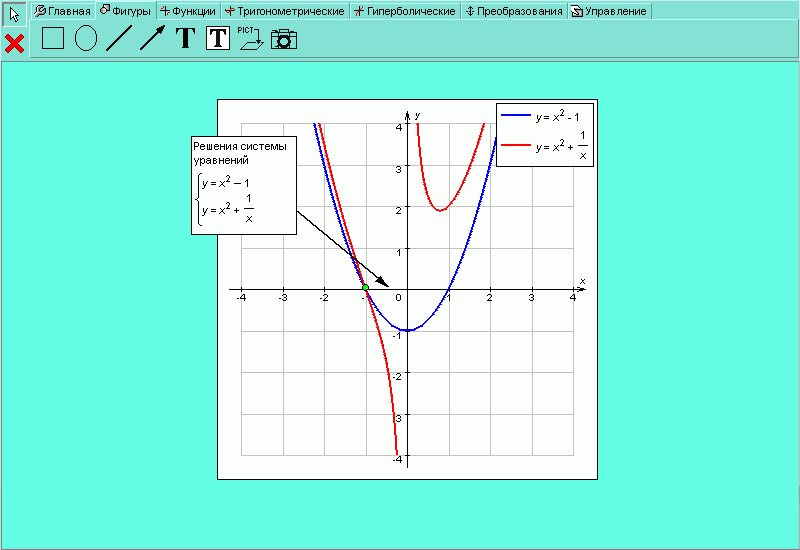
Аналогичным образом можно решать системы уравнений. На рисунке H.2.4.14 представлено графическое решение системы уравнений
|
| Рисунок H.2.4.1.14. Графическое представление решения системы уравнений
|
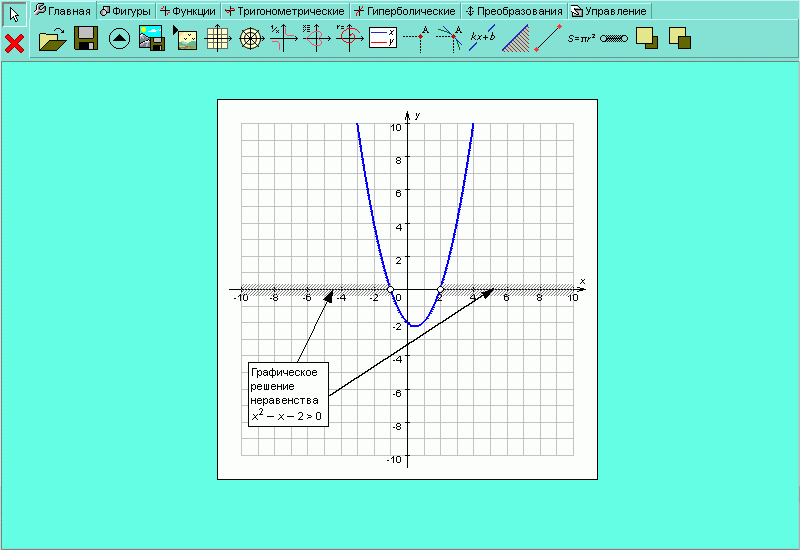
«Графер» имеет возможности, которые необходимы для графического представления решений неравенств и систем неравенств. Давайте получим графическое решение простейшего неравенства  Результат проделанных манипуляций представлен на рисунке H.2.4.15.
Результат проделанных манипуляций представлен на рисунке H.2.4.15.
|
| Рисунок H.2.4.1.15. Графическое представление решения неравенства
|
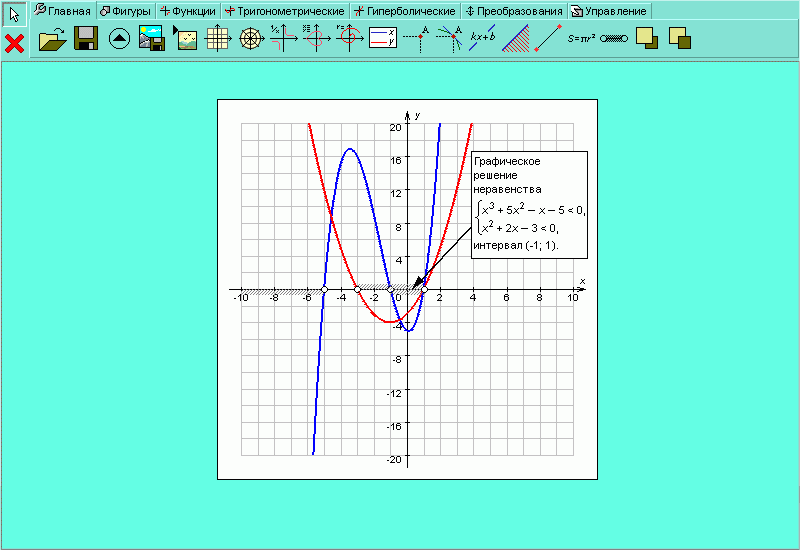
Давайте изобразим графически решение системы неравенств 
|
| Рисунок H.2.4.1.16. Графическое решение системы неравенств
|
Параметрические и полярные функции
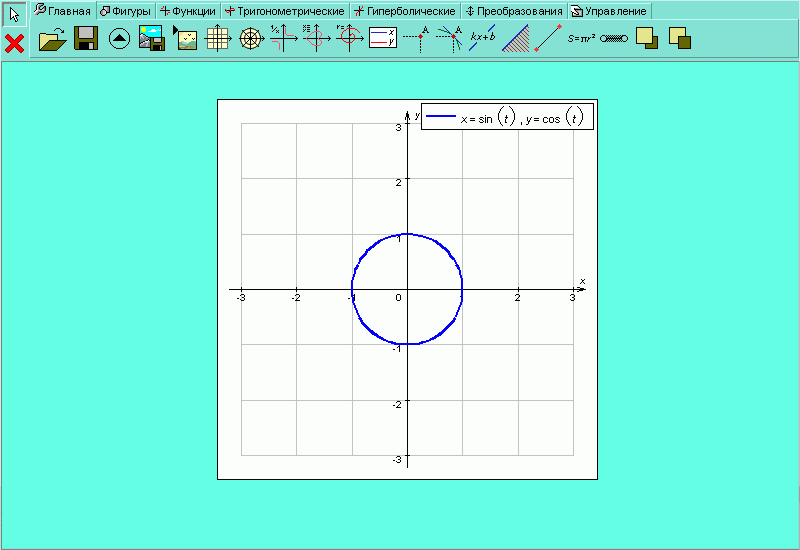
В некоторых случаях возникает необходимость построения графиков параметрических функций. Например, для графического изображения таких функций, в которых нельзя найти однозначную зависимость
|
| Рисунок H.2.4.1.17. График параметрической функции |
|
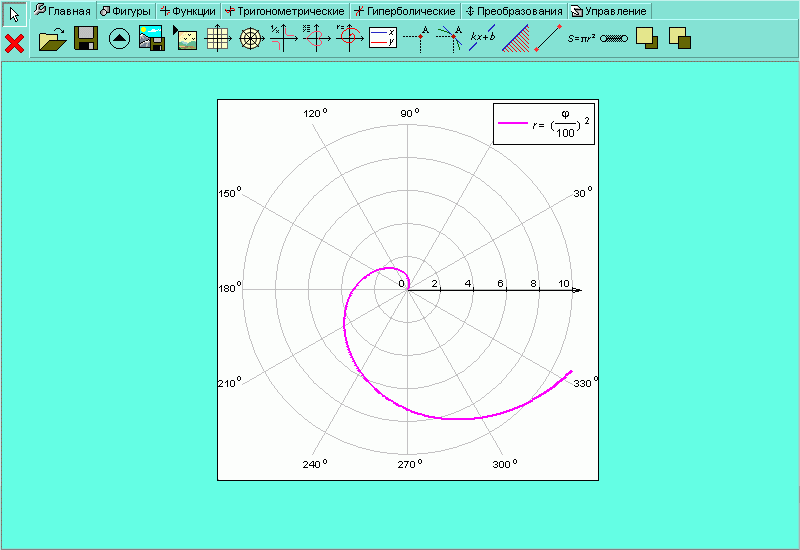
| Рисунок H.2.4.1.18. График функции |
 |
 |
 |

