Глава 3. Дифференцирование и интегрирование функций

3.4. Определенный интеграл

3.4.5. Определенные интегралы в физике

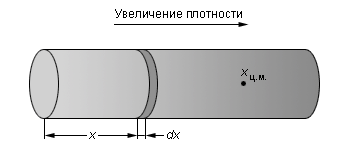
Мы уже упоминали, что интегральное исчисление применяется для нахождения пути, пройденного материальной точкой, по закону изменения его скорости. Какие еще задачи решают при помощи понятия интеграла в физике?

Модель 3.14. Движение с переменным ускорением

1. Пусть материальная точка движется с ускорением a (t). Тогда ее скорость равна
а перемещение –
где v₀, x₀ – постоянные, определяемые из начальных условий, t₀ и t – начальный и конечный моменты времени.

2.

1

Рисунок 3.4.5.1. Центр масс

Пусть плотность ρ (x) стержня с постоянным сечением S зависит от расстояния до начала стержня. Тогда масса стержня равна
где L – длина стержня, а центр масс стержня находится на расстоянии

3. Работа газа при его расширении от объема V₁ до объема V₂ равна
где P (V) – давление газа в этом процессе.

Модель 3.15. Работа газа