Пусть множество A состоит из p элементов, а множество B состоит из q элементов. Составим новое множество A × B, состоящее из всех упорядоченных пар (a, b), где a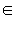A и bB.
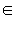Множество A × B называется декартовым произведением множествA и B.
Очевидно, что множество A × B содержит pq элементов.
Правило произведения: декартово произведение множеств A и B, содержащих p и q элементов соответственно, содержит pq элементов.
Для нас будет удобна следующая формулировка правила произведения.
Пусть некоторый объект a можно выбрать p способами, а объект b – q способами. Тогда количество способов, которыми можно выбрать упорядоченную пару (a, b), равно pq.
Правило произведения легко обобщается на большее число объектов.
Пример 1
Сколькими способами можно поставить на шахматную доску чёрную и белую ладью так, чтобы они не били друг друга?
Чёрную ладью можно поставить на шахматную доску p = 64 различными способами. Независимо от выбора поля чёрная ладья бьёт 15 полей, поэтому для второй ладьи остаётся 64 – 15 = 49 полей, то есть q = 49. Всего число возможных способов, по правилу произведения, равно pq = 64 ∙ 49 = 3136.
Ответ. 3136.
Пример 2
Сколько решений в натуральных числах имеет система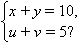
Число 10 можно представить в виде суммы двух слагаемых девятью различными способами: 1 + 9, 2 + 8, ..., 4 + 6, 5 + 5, 6 + 4, ..., 9 + 1. Заметим, что решения (a, b) и (b, a) мы считаем различными, и потому нам важен порядок, в каком число 10 представлено в виде суммы. Аналогично, число 5 можно представить в виде суммы двух натуральных слагаемых четырьмя различными способами. Каждому решению (x, y) можно выбрать в пару четыре решения (u, v). По правилу произведения, количество решений системы равно 9 ∙ 4 = 36.
Ответ. 36.
Пусть снова множество A состоит из p элементов, а множество B – из q элементов. Предположим, что множества A и B не пересекаются. В этом случае множество AB состоит из p + q элементов.
Это соображение и носит название правила суммы.
Обычно в задачах применяют оба правила вместе.
Пример 3
Встретились 6 друзей, и каждый пожал руку каждому. Сколько всего было рукопожатий?
Каждый пожал руку каждому, то есть каждый человек сделал 5 рукопожатий. Но общее количество рукопожатий получается по правилу суммы: n1 + n2 + ... + n6 = 6 × 5 = 30. Учтём теперь то, что каждое рукопожатие мы посчитали дважды, и получим в результате 15 рукопожатий.
