 |
 |
Дробь, знаменатель которой равен 10, 100, 1000 и вообще 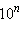 , может быть записана в виде десятичной дроби.
, может быть записана в виде десятичной дроби.
Например, 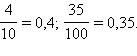 Аналогично можно записывать неправильную дробь и смешанное число, например
Аналогично можно записывать неправильную дробь и смешанное число, например 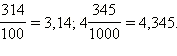 По сути, десятичное число – просто удобная форма записи дроби с указанными знаменателями.
По сути, десятичное число – просто удобная форма записи дроби с указанными знаменателями.
Рассмотрим десятичную дробь 3,1415. Имеем:
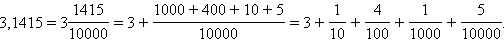 |
Таким образом, в десятичной дроби 3,1415 содержится 3 единицы, 1 десятая, 4 сотых, 1 тысячная, 5 десятитысячных. Вообще, в десятичной дроби может быть сколько угодно разрядов: десятые, сотые, тысячные, десятитысячные, стотысячные и т. д.
Рассмотренную дробь можно записать так:
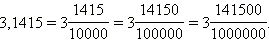 |
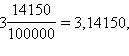 а
а 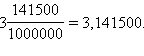 Таким образом, десятичная дробь не изменится, если к ней справа приписать любое количество нулей.
Таким образом, десятичная дробь не изменится, если к ней справа приписать любое количество нулей.
Ясно, что верно и обратное: десятичная дробь не изменится, если отбросить нули, стоящие справа в конце неё. Например, 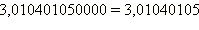 (нули, не стоящие в конце числа, отбрасывать нельзя).
(нули, не стоящие в конце числа, отбрасывать нельзя).
Перечислим, как с десятичными числами можно проводить известные нам арифметические операции.

 |
|
Модель 1.9.
Сложение и вычитание десятичных дробей
|
Сложение и вычитание. Сложение и вычитание десятичных чисел производится точно так же, как сложение и вычитание целых чисел, нужно только записывать одноимённые разряды один под одним. Например,
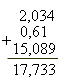 |
Умножение. Умножение десятичных дробей проводится следующим образом. Перемножаем данные числа, как целые, не обращая внимания на запятые. Затем ставим в произведении запятую по следующему правилу: число знаков после запятой в произведении равно сумме чисел знаков после запятой во всех сомножителях. Заметим, что до постановки запятой отбрасывать знаки нельзя.

 |
|
Модель 1.10.
Умножение и деление десятичных дробей
|
В частности, из этого правила следует, что десятичная дробь увеличится в 10, 100, 1000 и т. д. раз, если запятую перенести через один, два, три и т. д. разряда вправо.
Число 34,0945876 увеличится в 1000 раз, если мы напишем 34094,5876.
Десятичная дробь уменьшится в 10, 100, 1000 и т. д. раз, если запятую перенести через один, два, три и т. д. разряда влево.
Число 3409458,76 уменьшится в 100 раз, если мы напишем 34094,5876.
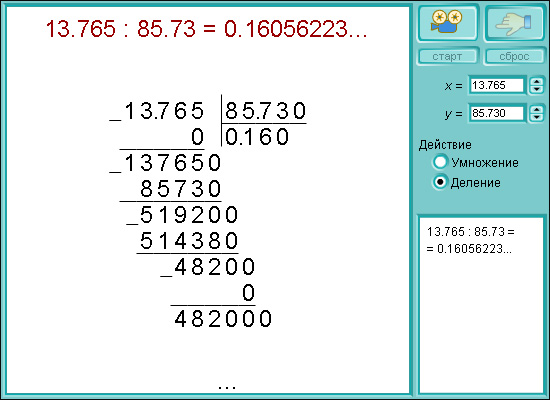
Деление. Деление десятичной дроби на натуральное число производится так же, как и натурального числа на натуральное. Запятую в частном ставят после того, как закончено деление целой части.
Если целая часть делимого меньше делителя, то в ответе получается нуль целых.
Для того чтобы разделить десятичную дробь (или целое число) на десятичное дробь, нужно отбросить запятую в делителе; в делимом же переносим запятую вправо на столько знаков, сколько их было в дробной части делителя (в случае необходимости в конце делимого приписывают нули). После чего делим полученное число на натуральное.
Пусть дана некоторая десятичная дробь, например 34,2741. Если приписать справа (после запятой) к ней любое число нулей, то, как известно, значение этой дроби не изменится:
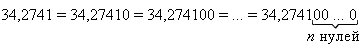 |
Если у десятичной дроби после запятой содержится бесконечно много знаков, то такая дробь называется бесконечной десятичной дробью. Справедлива важная теорема:
Любую обыкновенную дробь можно представить в виде бесконечной десятичной дроби. |
Рассмотрим, например, дробь 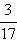 и будем делить числитель на знаменатель, постепенно получая десятичные знаки. При этом для нас будет важным то, что число 2 можно представить в виде 2,000...
и будем делить числитель на знаменатель, постепенно получая десятичные знаки. При этом для нас будет важным то, что число 2 можно представить в виде 2,000...
Получаем:
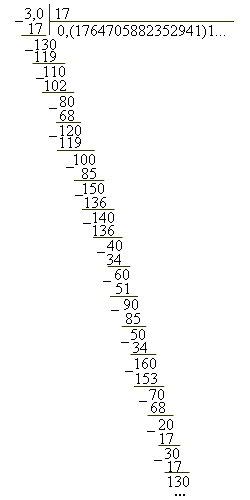 |
Значит, 
Если записать последовательно все получающиеся при этом делении остатки, то получится:
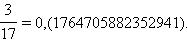 |

 |
|
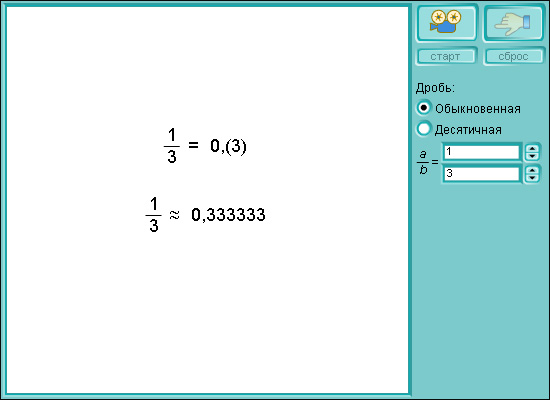
Модель 1.11.
Обыкновенные и десятичные дроби
|
Оказывается, что можно провести и обратную операцию, а именно, по любой десятичной дроби найти обыкновенную дробь, ей равную. Как это делается, покажем на примере.
Все дроби вида |
 |
 |
|
 |
 |
|
Выясним, как можно сравнивать десятичные дроби. Из всего вышесказанного следует, что сумма, разность, произведение и частное двух десятичных дробей снова будут десятичной дробью.
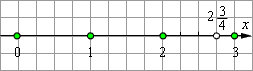
Говорят, что десятичная дробь 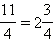 соответствует точка на числовой оси, которую можно получить следующим образом: нужно отложить вправо от начала координат единичный отрезок два раза, затем отложить ещё
соответствует точка на числовой оси, которую можно получить следующим образом: нужно отложить вправо от начала координат единичный отрезок два раза, затем отложить ещё 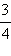 длины этого отрезка. Если рассмотреть точку, симметричную данной относительно начала координат, то получим точку, которая соответствует числу
длины этого отрезка. Если рассмотреть точку, симметричную данной относительно начала координат, то получим точку, которая соответствует числу 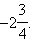
 |
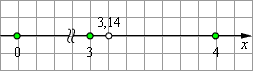
Аналогично можно поступить с десятичными дробями. Так, десятичному числу 3,14 отвечает точка на координатной прямой, которая получается следующим образом. Нужно от начала координат отложить три раза единичный отрезок, после отложить один раз отрезок длины 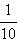 от единичного; затем отложить отрезок длины
от единичного; затем отложить отрезок длины 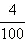 единичного. Полученная точка и соответствует числу 3,14.
единичного. Полученная точка и соответствует числу 3,14.
 |
 |
 |
 |


| Производство рти |
| производства - высокое качество в кратчайшие сроки |
| rti-project.ru |