
Учебник. Инверсия
Определим преобразование точек плоскости следующим образом. Пусть задана окружность
Каждой точке A плоскости, отличной от O, поставим в соответствие точку
на луче OA, такую, что
Соответствие между точками плоскости, заданное соотношением (1), является взаимно однозначным преобразованием всех точек плоскости, за исключением точки O – центра окружности
Действительно, пусть A – некоторая точка плоскости, отличная от точки O. Тогда пара точек {O; A} определяет единственный луч OA и отрезок OA. Найдем из соотношения (1) В соответствии с аксиомой 1.5 существует единственная точка на луче OA, такая, что В соответствии с определением данное соответствие есть преобразование точек плоскости. В силу симметрии соотношения (1) относительно сомножителей OA и точно такие же рассуждения можно привести относительно единственности точки A при заданном Отсюда следует, что соответствие, заданное соотношением (1), – взаимно однозначное преобразование.
Это преобразование называется преобразованием инверсии или просто инверсией относительно окружности Обозначим ее Образ точки O при инверсии не определен. Точка O называется центром инверсии, а R – радиусом инверсии.
В определении инверсии выражение (1) симметрично относительно сомножителей, что позволяет трактовать точку A как образ точки при инверсии Сформулируем на этой основе следующее свойство инверсии.
Если точке A при инверсии соответствует точка то точке соответствует точка A, то есть если то верно
Точки A и A1 называют взаимно обратными точками.
С учетом определения обратного преобразования это свойство можно записать так: преобразование инверсии и обратное к нему преобразование совпадают
Вспоминая, что где e – тождественное преобразование, получим окончательно
Очевидно, что если то OA = R, и из (1) имеем то есть и, следовательно,
При инверсии относительно каждая точка окружности неподвижна.
В остальных случаях из пары связанных инверсий точек одна лежит внутри окружности другая – вне этой окружности.
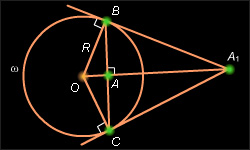
Пусть – заданная окружность (рис. 12.8.1). Пусть точка A лежит внутри окружности и где и Проведем через точки B и C касательные к окружности, которые пересекутся с лучом [OA) в точке Покажем, что
Действительно, из того свойства, что высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому отрезков гипотенузы, полученных разбиением ее основанием высоты, получаем, что
но
откуда
Если две фигуры F и имеют единственную общую точку, то их образы при инверсии также будут иметь единственную общую точку.
Пусть – единственная общая точка фигур F и а – образ точки A при инверсии Если и то очевидно, Допустим, что существует еще какая-либо общая для фигур и точка отличная от точки и B – ее прообраз. Но в силу теоремы 12.24 и и, следовательно, и по условию B = A. Но тогда одновременно должны быть верны соотношения что противоречит взаимной однозначности инверсии.
Введем далее прямоугольную систему координат OXY с началом в центре окружности инверсии (рис. 12.8.2).
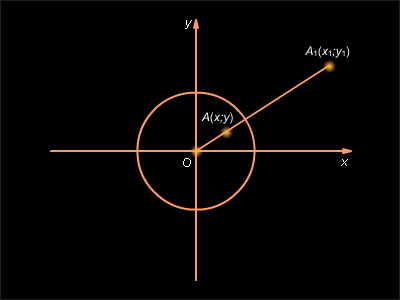
Пусть
– прообраз точки
при инверсии
Из рисунка ясно, что
Отсюда имеем
Инверсия преобразует:
- прямую, проходящую через центр инверсии, в эту же прямую;
- прямую, не проходящую через центр инверсии, в окружность, проходящую через центр инверсии;
- окружность, проходящую через центр инверсии, в прямую, не проходящую через центр инверсии;
- окружность, не проходящую через центр инверсии, в окружность, не проходящую через центр инверсии.
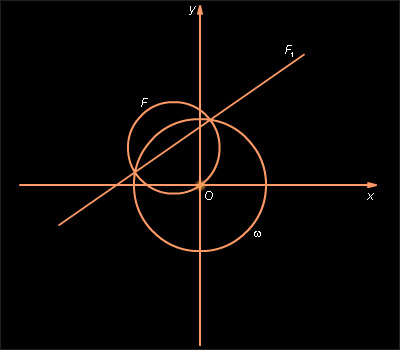
Рассмотрим фигуру F, задаваемую уравнением
Рассмотрим различные случаи, перечисленные в условии теоремы.
- Пусть A = D = 0, тогда исходное уравнение определяет прямую F: Bx + Cy = 0. При этом уравнение (5) имеет вид что также задает прямую F (рис. 12.8.3).
-
F – прямая, не проходящая через точку O. Тогда A = 0, D ≠ 0 и уравнение для F примет вид
-
F – окружность, проходящая через точку O. Тогда A ≠ 0, но D = 0, и уравнение (4) имеет вид
-
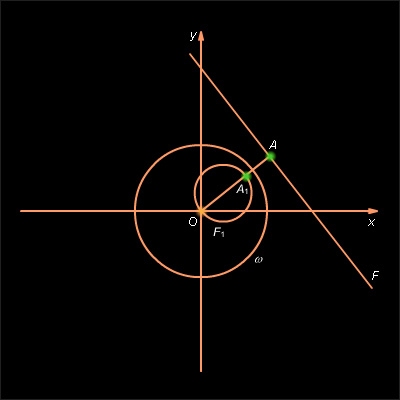
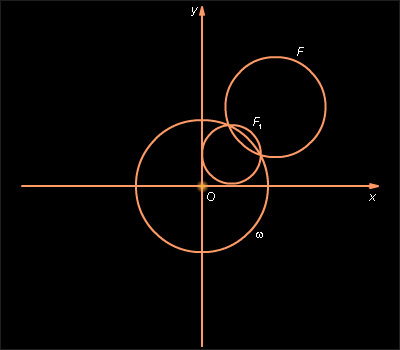
F – окружность, не проходящая через точку O. В этом случае A ≠ 0, D ≠ 0. Действительно, тогда уравнение (4) можно записать в виде
(6) Но при преобразовании инверсии уравнение, задающее имеет тот же вид, что и исходное уравнение (4), и, следовательно, может быть приведено к виду (6) (рис. 12.8.6).
|
|
|
|
|
|
Назовем углом между пересекающимися окружностями с вершиной в точке пересечения меньший угол между касательными к ним прямыми в точке пересечения. Аналогично углом между окружностью и пересекающей ее прямой с вершиной в точке пересечения называется угол между этой прямой и касательной к окружности, проведенной в точке пересечения. Из этого определения следует, что если две окружности или прямая и окружность касаются (то есть имеют единственную общую точку), то угол между ними равен нулю.
При инверсии углы сохраняются.
Заметим, что образом прямой при инверсии является либо окружность, либо прямая, и наоборот, прообразом прямой в силу теоремы 12.24 также является либо прямая, либо окружность. Отсюда и на основании определений, приведенных выше, следует, что образом угла (так же, как и его прообразом) является угол, сторонами которого в общем случае являются касательные к соответствующим окружностям. Поэтому достаточно рассмотреть доказательство для случая двух прямых и не проходящих через центр инверсии. При этом возможны два случая: либо угол между прямыми равен нулю, либо угол отличен от нуля.
Первый случай возникает, во-первых, когда прямые и совпадают, и, во-вторых, когда прямая и окружность (или две окружности) касаются. В случае совпадений прямых их образы, очевидно, также совпадают, и, следовательно, значение угла между прямыми сохраняется. Если же имеет место случай касания, то по лемме 12.1 их образы при инверсии также касаются. Действительно, поскольку исходные фигуры касаются, то они имеют единственную общую точку и по лемме 12.1 их образы также имеют единственную общую точку, то есть касаются, и, следовательно, угол между прямыми равен нулю.
Во втором случае прямые и пересекаются в некоторой точке A, отличной от центра инверсии. Тогда образами прямых и будут окружности и которые пересекаются в точке O (см. теорему 12.26) и еще в некоторой точке Поскольку углы между окружностями в точках O и B равны, можно рассмотреть угол в точке O. Касательные прямые и в точке O к окружностям и параллельны прямым и соответственно. Докажем это. Рассмотрим прямую касающуюся окружности в точке C. Пусть – ее прообраз при инверсии относительно окружности В силу теоремы 12.25 а по теореме 12.26 – и OC = R. Рассмотрим окружность где – середина отрезка OC, а Покажем, что (рис. 12.8.7).

Действительно, выберем произвольную точку
Пусть
Треугольник
– прямоугольный по построению окружности
Угол
– прямой, как вписанный в окружность
и опирающийся на диаметр OC. Тогда по свойству высоты, опущенной на гипотенузу, имеем
но
Учтем, что
и получим
По условию, прямые l и параллельны, и поэтому у них нет общих точек. Поэтому их образы при инверсии относительно также не имеют общих точек, кроме точки O. Следовательно, и касаются в точке O, и касательные и совпадают. Отсюда следует, что Аналогично Следовательно, угол между прямыми и совпадает с углом между двумя прямыми и Теорема доказана.
Пусть
и
– образы точек A и B соответственно при инверсии с центром O и радиусом R. Тогда треугольники OAB и
подобны и
По определению инверсии выполняются равенства
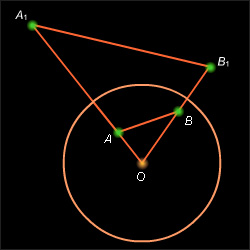
Отсюда следует, что
Из этого равенства
Теорема Птолемея. Произведение диагоналей вписанного в окружность четырехугольника равно сумме произведений противоположных его сторон.
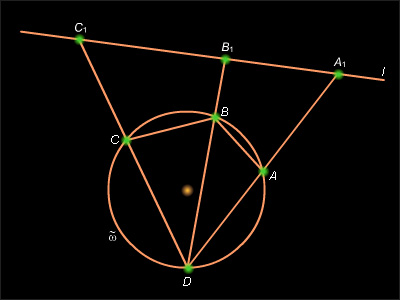
Пусть четырехугольник ABCD вписан в окружность
(рис. 12.8.9). Рассмотрим инверсию
с центром в точке D. Образом окружности
при этой инверсии (с некоторым радиусом R) будет прямая l, не содержащая точку D. Пусть
и
Тогда
По лемме 12.2
и
Подставим эти выражения в равенство и получим
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".