Учебник. Подобие треугольников

Пусть у треугольников ABC и $A_1{B}_1{C}_1$  $\angle A=\angle A_1$  $\angle B=\angle B_1$ Пусть $\frac{AB}{A_1{B}_1}\mathrm{.}$   Переведем треугольник $A_1{B}_1{C}_1$ гомотетией f с любым центром и коэффициентом k в треугольник $A_2{B}_2{C}_2$ (см. рис. 12.7.1).

Первый признак подобия треугольников

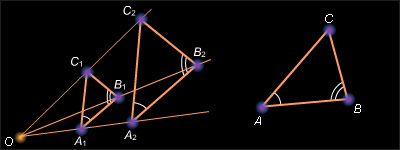
Треугольники ABC и A₂B₂C₂ равны и, следовательно, подобны. Действительно, при гомотетии углы сохраняются, значит, $\angle A_1=\angle A_2=\angle A$  $\angle B_1=\angle B_2=\angle B$ Кроме того A₂B₂ = kA₁B₁ = AB. По второму признаку равенства треугольники ABC и A₂B₂C₂ равны (теорема 4.2). По теореме 12.6 существует движение g, переводящее $\Delta A_2{B}_2{C}_2$ в $\Delta \mathrm{.}$   Выполнив сначала гомотетию f, а затем движение g, мы осуществим подобие g ˆ f, которое переводит треугольник $A_1{B}_1{C}_1$ в треугольник ABC. Следовательно, $\Delta \mathrm{.}$   Теорема доказана.

Пусть у треугольников ABC и $\Delta A_1{B}_1{C}_1$  $\angle C=\angle C_1$ и $AC=k{A}_1{C}_1$   $BC=k{B}_1{C}_1$ Докажем, что $\Delta \mathrm{.}$   Переведем треугольник A₁B₁C₁ гомотетией f с любым центром и коэффициентом k в треугольник A₂B₂C₂. ΔA₂B₂C₂ = ΔABC. Действительно, $A_2{C}_2=k{A}_1{C}_1=AC$  $B_2{C}_2=k{B}_1{C}_1=BC$  $\angle C_2=\angle C_1=\angle C$ Треугольники $A_2$ и ABC равны по первому признаку равенства треугольников (теорема 4.1). По теореме 12.6 существует движение g, переводящее ΔA₂B₂C₂ в ΔABC. Выполнив сначала гомотетию f, а затем движение g, получим подобие g ˆ f, которое переводит ΔA₁B₁C₁ в ΔABC. Следовательно, $\Delta \mathrm{.}$   Теорема доказана.

Пусть у треугольников ABC и A₁B₁C₁ AB = kA₁B₁, BC = kB₁C₁, AC = kA₁C₁. Переведем треугольник A₁B₁C₁ гомотетией f с произвольным центром O и коэффициентом k в треугольник A₂B₂C₂. При этом

A₂B₂ = kA₁B₁ = AB, A₂C₂ = kA₁C₁ = AC, B₂C₂ = kB₁C₁ = BC. По третьему признаку треугольники ABC и ΔA₂B₂C₂ – равны (теорема 4.7). Если g – движение, переводящее ΔA₂B₂C₂ в ΔABC, то преобразование g ˆ f – подобие, переводящее ΔA₁B₁C₁ в ΔABC. Следовательно, $\Delta \mathrm{.}$   Теорема доказана.