Открытая Математика. Планиметия. Симметрия и поворот

Симметрия и поворот

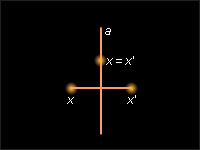
Точки X и $X^{′}$ называются симметричными относительно прямой a, и каждая из них – симметричной другой, если a является серединным перпендикуляром отрезка $X X^{′}$ (см. рис. 12.4.1). Очевидно, что если дана прямая a, то каждой точке X соответствует единственная точка $X^{′},$ симметричная относительно a. Кроме того, множеством неподвижных точек преобразования симметрии относительно прямой a является эта прямая a.

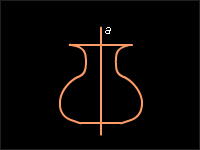
Преобразованием симметрии относительно прямой a (или осевой симметрией с осью a) называется такое преобразование фигуры F (см. рис. 12.4.2), при котором каждой точке данной фигуры сопоставляется точка, симметричная ей относительно прямой a. Обозначим $F^{′} = S_{a} (F),$ a – ее ось симметрии. Фигура называется симметричной относительно прямой a, если фигура симметрична сама себе (см. рис. 12.4.3), то есть $F = S_{a} (F) .$

Замечание. Поскольку симметричность точек относительно прямой взаимна, то фигуры F и $F^{′}$ называются симметричными относительно прямой a.


Симметрия точек относительно прямой		Симметрия треугольников		Симметрия фигур

Преобразование симметрии относительно прямой является движением.

Примем данную прямую за ось OY декартовой системы координат. Пусть произвольная точка $A (x; y)$ переходит в точку $A^{′} (x^{′}; y^{′}) .$ Из определения симметрии относительно прямой следует, что у точек A и $A^{′}$ равные ординаты и противоположные абсциссы: $y^{′} = y, x^{′} = - x .$ Рассмотрим произвольные точки $A (x_{1}; y_{1})$ и $B (x_{2}; y_{2}),$ которые перейдут в точки $A^{′} (- x_{1}; y_{1})$ и $B^{′} (- x_{2}; y_{2}) .$ Имеем: $A B^{2} = {(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2},$ $A^{′} B^{′2} = {(- x_{2} + x_{1})}^{2} + {(y_{2} - y_{1})}^{2} .$ Отсюда видно, что $A B = A^{′} B^{′} .$ Это значит, что преобразование симметрии относительно прямой есть движение. Теорема доказана.

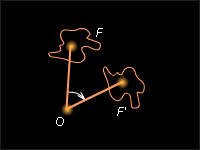
Поворотом фигуры F вокруг центра O на данный угол φ (0° ≤ φ ≤ 180°) в данном направлении называется такое ее преобразование, при котором каждой точке X ∈ F сопоставляется точка $X^{′}$ так, что $O X = O X^{′}, ∠ X O X^{′} = φ$ и луч $O X^{′}$ откладывается от луча OX в заданном направлении. Точка O называется центром поворота, а угол φ – углом поворота (рис. 12.4.4). Множеством неподвижных точек преобразования поворота является центр поворота.

Поворот фигуры

Поворот является движением.

Пусть при повороте вокруг точки O точкам X и Y сопоставляются точки $X^{′}$ и $Y^{′}$ (рис. 12.4.5).

К теореме 12.11

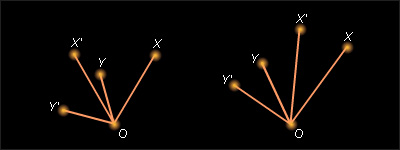
Очевидно, $\overset{⟶}{O X} + \overset{⟶}{X Y} = \overset{⟶}{O Y}$ и $\overset{⟶}{O X^{′}} + \overset{⟶}{X^{′} Y^{′}} = \overset{⟶}{O Y^{′}}$ по теореме 11.6. Откуда $\overset{⟶}{X Y} = \overset{⟶}{O Y} - \overset{⟶}{O X}, \overset{⟶}{X^{′} Y^{′}} = \overset{⟶}{O Y^{′}} - \overset{⟶}{O X^{′}} .$ Из этих равенств имеем: ${| \overset{⟶}{X Y} |}^{2} = {| \overset{⟶}{O Y} |}^{2} + {| \overset{⟶}{O X} |}^{2} - 2 (\overset{⟶}{O Y} ċ \overset{⟶}{O X}) = {| \overset{⟶}{O Y} |}^{2} + {| \overset{⟶}{O X} |}^{2} - 2 | \overset{⟶}{O X} | | \overset{⟶}{O Y} | cos α,$ ${| \overset{⟶}{X^{′} Y^{′}} |}^{2} = {| \overset{⟶}{O Y^{′}} |}^{2} + {| \overset{⟶}{O X^{′}} |}^{2} - 2 (\overset{⟶}{O Y^{′}} ċ \overset{⟶}{O X^{′}}) = {| \overset{⟶}{O Y^{′}} |}^{2} + {| \overset{⟶}{O X^{′}} |}^{2} - 2 | \overset{⟶}{O X^{′}} | | \overset{⟶}{O Y^{′}} | cos β,$ где α = ∠XOY, $β = ∠ X^{′} O Y^{′} .$ Но по определению поворота $| \overset{⟶}{O Y} | = | \overset{⟶}{O Y^{′}} |, | \overset{⟶}{O X} | = | \overset{⟶}{O X^{′}} | .$ Кроме того, $∠ X O Y \pm ∠ Y O X^{′} = ∠ X O X^{′}$ и $\pm ∠ Y O X^{′} + ∠ X^{′} O Y^{′} = ∠ Y O Y^{′} .$ Знаки «+» или «–» выбираются соответственно, если OY лежит между OX и $O X^{′}$ и если OY не лежит между $O X^{′}$ и OX. Но по определению $∠ Y O Y^{′} = ∠ X O X^{′}$ – углу поворота. Отсюда $∠ X O Y = ∠ X^{′} O Y^{′}$ или α = β. В итоге получаем ${| \overset{⟶}{X Y} |}^{2} = {| \overset{⟶}{X^{′} Y^{′}} |}^{2},$ откуда $X Y = X^{′} Y^{′} .$ Следовательно, по определению поворот – движение. Теорема доказана.

Точки X и $X^{′}$ называются симметричными относительно заданной точки O, если $O X = O X^{′},$ а лучи OX и $O X^{′}$ являются дополнительными. Точка O считается симметричной самой себе.

Преобразованием симметрии (или центральной симметрией) относительно точки O называется такое преобразование фигуры F, при котором каждой ее точке X сопоставляется точка $X^{′},$ симметричная относительно точки O. Обозначается $F^{′} = S_{0} (F) .$ Фигура называется симметричной относительно точки O или центрально-симметричной, если она симметрична сама себе относительно точки O. Точка O называется центром симметрии.

Центральная симметрия является движением.

Справедливость теоремы следует из того, что центральная симметрия есть поворот на 180°, и теоремы 12.11.

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Симметрия и поворот

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ