
Учебник. Неравенства и геометрические фигуры
Фигуры на плоскости могут задаваться не только уравнениями, но и неравенствами. Например, на оси абсцисс неравенство x ≥ a задает луч с началом в точке A (a; 0), а неравенство b ≤ x ≤ c – отрезок AB с концами A (b; 0) и B (c; 0).
Будем говорить, что фигура F задается данным неравенством в плоскости Oxy, если точка принадлежит фигуре F тогда и только тогда, когда координаты этой точки удовлетворяют данному неравенству.
Неравенство ax + by + c > 0 задает полуплоскость.
Пусть A1 (x1; y1) и A2 (x2; y2) – точки, координаты которых удовлетворяют исходному неравенству:
Покажем, что все точки этой полуплоскости удовлетворяют исходному неравенству. Допустим противное, а именно: существует точка A0 (x0; y0) полуплоскости, координаты которой не удовлетворяют исходному неравенству. Тогда либо ax0 + by0+ c = 0, либо ax0 + by0 + c < 0. В первом случае точка (x0; y0) лежит на прямой, разбивающей плоскость на две полуплоскости, и по определению не принадлежит ни одной из них, и мы приходим к противоречию с предположением. Во втором случае с учетом исходного неравенства ax1 + by1 + c > 0 для точки A1 имеем, во-первых, что (ax1 + by1 + c) / (a (x1 – x0) + (y1 – y0)) < 1, во-вторых, что a (x0 – x1) + b (y0 – y1) < 0. Рассмотрим отрезок A0A1. Точки этого отрезка удовлетворяют равенствам: x = x1 + λ (x0 – x1), y = y1 + λ (y0 – y1). Умножим первое равенство на a, второе – на b, сложим и прибавим к обоим частям c. В результате получим равенство ax + by + c = ax1 + by1 + c + λ (a (x0 – x1) + b (y0 – y1)). Приравняем обе части равенства к нулю. Равенство нулю правой части дает значение λ = (ax1 + by1+ c) / (a (x1 – x0) + (y1 – y0)). C учетом ранее полученных неравенств имеем: 0 < λ < 1. Это значит, что точка (x; y) принадлежит отрезку A0A1. С другой стороны, равенство ax + by +c = 0 означает, что точка (x; y) лежит на прямой, разбивающей плоскость на две полуплоскости. То есть отрезок A0A1 пересекает прямую, разбивающую плоскость на две полуплоскости, следовательно, точки A0 и A1 лежат в разных полуплоскостях. Полученное противоречие доказывает теорему.
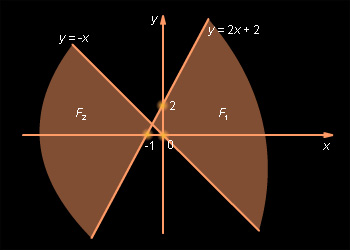
Для примера изобразим фигуру, задаваемую неравенством (x + y)(2x – y + 2) > 0. Это неравенство эквивалентно объединению двух систем неравенств:
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".