Перпендикулярность прямых и плоскостей
Задачи с решениями
Прямоугольник ABCD имеет стороны 15 см и 20 см. Он согнут по диагонали AC так, чтобы плоскости ABC и ADC стали взаимно перпендикулярными. Найти длину отрезка BD после этого сгибания.
Решение
Шаг 1
Изображаем данный прямоугольник ABCD после сгибания. Произведем маркировку рисунка. Примем согласно условию, что AB = 20, CB = 15. Тогда DC = 20, DA = 15,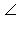 
ABC = 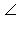ADC = 90°. Полученная после сгибания фигура представляет собой пирамиду BACD.
Шаг 2
В пирамиде BACD четыре ребра известны. (AB = CD = 20, BC = AD = 15). Длина ребра AC легко находится из прямоугольного треугольника ABC по теореме Пифагора. AC2 = AB2 + BC2 = 202 + 152 = 625, откуда AC = 25. Требуется найти длину ребра BD.
Шаг 3
Обычно длину отрезка находят из треугольника. Если этот треугольник прямоугольный, то применяют теорему Пифагора, если этот треугольник не прямоугольный, применяют теорему косинусов. Проведем высоту BE треугольника ABC. Согласно теореме 9 (глава 3) прямая BE перпендикулярна плоскости ADC. Значит, 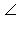BED = 90°, и можно искать длину отрезка BD из прямоугольного треугольника BDE.
Шаг 4
Ищем BE. Из прямоугольного ΔBCE имеем:
Шаг 5
Ищем DE. Из прямоугольного ΔBCE имеем:
Шаг 6
Из треугольника DCE по теореме косинусов находим отрезок DE.
Шаг 7
Из прямоугольного ΔBDE по теореме Пифагора получаем: BD2 = BE2 + DE2 = 122 + 193 = 337 и 
Ответ:
Замечание.
Приведем другое решение. Согласно формуле трех косинусов (глава 3 пункт 3.5)
Теперь из
ΔBCD по теореме косинусов имеем:
BD2 = BC2 + DC2 – 2BC·DC · cos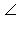BCD,
и
15 из 19
 |
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".
