Задачи с решениями

На чертеже изображена данная окружность и данные радиусы AO и BO. Пусть MQ – искомая хорда (MN = NP = PQ).

Анализ. Пусть радиус 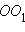делит угол 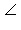AOB пополам.

Через точку O₁ проведем касательную к окружности. Продолжим отрезки AO и BO до пересечения с этой касательной и получим точки A₁ и B₁ соответственно.

Строим на прямой A₁B₁ точки M₁ и Q₁, такие, что A₁M₁ = A₁B₁ = B₁Q₁. Отметим, что точка M лежит на отрезке OM₁, а точка Q лежит на отрезке OQ₁.

Построение. Строим точку O₁ – середину дуги AB. Через точку O₁ проводим касательную к окружности.

Продолжаем отрезки OA и OB до пересечения с этой касательной. Пусть A₁ и B₁ – точки пересечения касательной и продолжений отрезков OA и OB соответственно.

Строим на прямой A₁B₁ точки M₁ и Q₁ так, чтобы M₁A₁ = A₁B₁ = B₁Q₁ и M₁Q₁ = 3·A₁B₁. Проводим отрезки OM₁ и OQ₁.

Точки M и Q пересечения отрезков OM₁ и OQ₁ с окружностью и будут концами искомой хорды MQ

Доказательство. Гомотетия с центром O и коэффициентом 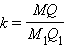 переводит отрезок 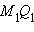в отрезок MQ. Так как M₁A₁ = A₁B₁ = B₁Q₁, то, из свойств гомотетии, MN = NP = PQ, где N, P – точки пересечения хорды MQ и радиусов AO и BO соответственно.