Глава 8. Построение фигур
8.8. Деление отрезка на n равных частей
Разделить данный отрезок AB на n равных частей.
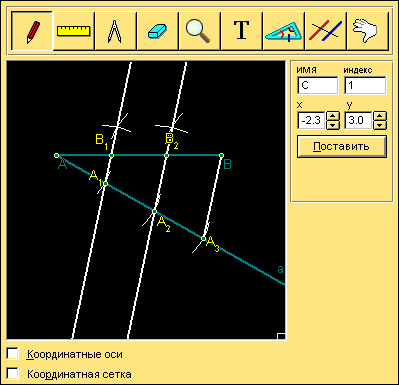
Построение. Пусть [AB] – данный отрезок. Проведем из точки A луч a, не содержащий отрезок AB. Отложим от точки A на построенном луче равные отрезки: AA1, A1A2, ... , An – 1An. Соединим точки Anи B. Проведем через точки A1, A2, ... , An – 1 прямые, параллельные прямой AnB (см. § 8.6). Они пересекают отрезок AB в точках B1, B2, ... , Bn – 1. Отрезки AB1, B1B2, ... , Bn – 1B – искомые отрезки.

 |
|
Модель 8.10.
Деление отрезка на равные части
|
Равенство отрезков AB1 = B1B2 = ... = Bn – 1B следует непосредственно из теоремы Фалеса.
 1
|
| Рисунок 8.8.1. Деление отрезка на n равных частей.
|
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".








