 |
 |

|
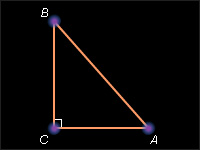
| Рисунок 4.5.1 |


Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
 |
 |
 |

