Глава 1. Точка и прямая
1.3. Луч
Лучом называется часть прямой, состоящая из всех точек, которые лежат по одну сторону от фиксированной точки прямой, и самой этой точки, называемой началом луча. Разные лучи одной прямой с общим началом называются дополнительными. Лучи AB и AC, изображенные на рис. 1.3.1, являются дополнительными.
Для обозначения луча будем использовать либо строчную букву латинского алфавита a, b, ..., z как и для прямой, либо символ [AB), где A – начало луча, а B – точка лежащая на луче.
Свойство луча определяется аксиомой:
Аксиома 1.5.
На любом луче от его начальной точки можно отложить отрезок заданной длины, и только один.
На основании свойств отрезка и луча можно доказать следующее утверждение:
Если на луче отложить от начальной его точки A два отрезка AB и AC и если AB = AC, то точки B и C совпадут.
 1
|
| Рисунок 1.3.1. Луч
|
 2
|
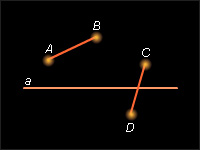
| Рисунок 1.3.2. Взаимное расположение прямых и отрезков
|
Говорят, что две точки A и B, не лежащие на данной прямой, лежат по одну сторону от нее, если отрезок AB не пересекает данную прямую. Совокупность всех точек, лежащих по одну сторону от прямой, называется полуплоскостью.
После введения новых понятий (отрезок, полуплоскость) сформулируем еще одно свойство прямой:
Аксиома 1.6.
Прямая разбивает плоскость на две полуплоскости.
Следствие 1.2.
Можно доказать, что если точки C и D лежат в разных полуплоскостях от прямой a, то отрезок CD пересекает прямую a.
Верны следующие теоремы:
Теорема 1.1.
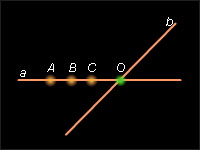
Если точки O, A, B, C лежат на прямой a так, что A и B лежат по одну сторону от точки O, точки B и C также лежат по одну сторону от точки O, тогда точки A и C лежат по одну сторону от точки O.
Проведем через точку O прямую b, отличную от a. Она разбивает плоскость на две полуплоскости. Одной из них принадлежит точка B. Так как отрезки AB и BC не пересекают прямую b, то точки A и C принадлежат той же полуплоскости, что и B. Тогда отрезок AC не пересекает прямую b и, следовательно, не содержит точку O. То есть точки A и C лежат по одну сторону от точки O.
 3
|
| Рисунок 1.3.3. К теореме 1.1
|
|
Лемма 1.1.
Если точки O, A, B, C лежат на прямой a, причем точка A лежит между точками O и B, а точка B лежит между точками O и C, то точки A, B и C лежат по одну сторону от точки O.
Так как по условию точка A лежит между точками O и B, то точки A и B лежат по одну сторону от точки O. В силу второго условия точки C и B также лежат по одну сторону от точки O. Следовательно, по теореме 1.1 все три точки A, B, C лежат по одну сторону от точки O. Лемма доказана.
|
Теорема 1.2.
Если точки O, A, B, C лежат на прямой a так, что точка A лежит между точками O и B, а точка B – между точками O и C, тогда точка B лежит между точками A и C.
Доказательство теоремы проведем методом от противного. Предположим, что из данного условия теоремы заключение не следует, то есть B не лежит между точками A и C. Следовательно, по свойству взаиморасположения точек A, B, C точки A и C лежат по одну сторону от точки B. Так как по лемме 1.1 все три точки лежат по одну сторону от точки O, то либо точки A, C, O лежат по одну сторону от точки B, что противоречит условию того, что O и C лежат по разные стороны от точки B, либо точки A и C лежат по другую сторону от точки B нежели точка O. Но это противоречит условию принадлежности точки A отрезку OB. Полученное противоречие показывает, что предположение о том, что точка B не лежит между точками A и C неверно: это приводит к противоречию с условием теоремы. Следовательно, точка B лежит между точками A и C, что и доказывает теорему.
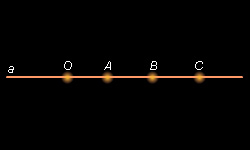 4
|
| Рисунок 1.3.4. Взаимное расположение точек на прямой
|
|
 |
 |
 |


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".














