Задачи с решениями

Даны четыре точки O, A, B, C. Точка O лежит между точками A и C, и точка O лежит между точками A и B.
а) Лежат ли они на одной прямой?
б) Лежат ли точки B и C на одном луче с началом в точке O? Изобразите возможное расположение данных точек на плоскости.

Из условия ясно, что O[A, B], O[A, C]. Отсюда следует, что отрезки AB и AC имеют две общие точки A и O. По аксиоме 2.2 существует единственная прямая, содержащая точки A и O, а следовательно, и отрезки AB и CA. Таким образом, все четыре точки лежат на одной прямой. По условию точки O и C лежат по одну сторону от точки A. По теореме 1.2 точки B и C лежат по одну сторону от точки A.

Рассмотрим три точки O, B, C. Предположим, что точка O лежит между точками B и C. Тогда BO + OC = BC (*) и получим 2·AO + OB + OC = AC + AB. C учетом (*) и того, что AC + AB = CA + AB = CB = BC, имеем 2·AO + BC = BC или AO = 0. Это противоречит условию. Следовательно, точки B и C лежат по одну сторону от точки O. Отсюда следует, что точки B и C лежат на одном луче с началом в точке O.

Чтобы изобразить расположение точек, построим произвольную прямую a и отметим на ней точки A и O. B соответствии с условием построим точку B на луче, дополняющем луч OA. На основании доказанного точка C лежит на луче OB либо по одну, либо по разные стороны от точки B с точкой O.

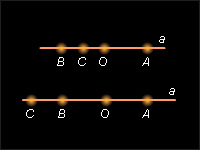
1 из 5