Глава 1. Точка и прямая

1.1. Точка, прямая

Поскольку каждая геометрическая фигура состоит из точек, можно говорить о точках, принадлежащих геометрической фигуре (то есть о точках, из которых она состоит) и не принадлежащих ей. Для обозначения точек будем использовать заглавные буквы латинского алфавита: A, B, ..., Z, а для обозначения прямой – строчные буквы: a, b, ..., z. Кроме того будем использовать обозначение (AB) для прямой, проходящей через две заданные точки A и B.

Так, о точке A, принадлежащей прямой a, говорят, что точка A лежит на прямой a. Так же правильно будет, если скажут, что прямая a содержит точку A или прямая a проходит через точку A. А о точке B, не принадлежащей прямой a, говорят либо, что точка B не лежит на прямой a, либо, что прямая a не содержит точку B, либо, что прямая a не проходит через точку B.

Для того чтобы говорить о той или иной геометрической фигуре, мы должны уметь отличать одну фигуру от другой. Это можно сделать, если, например, мы сможем описать такие ее свойства, которые присущи только данной фигуре и которыми не обладает более ни одна другая фигура.

1

Рисунок 1.1.1. Взаимное расположение точек и прямых

Часть свойств прямой, которые позволят определить ее таким образом, задаются с помощью следующих двух аксиом:

Описав частично свойства прямой, мы можем уже сделать некоторые заключения. Например, выберем две точки. По аксиоме 1.2 эти две точки задают единственную прямую a. Выберем теперь еще две точки так, чтобы хотя бы одна из них (пусть это будет точка A) не лежала на заданной прямой a. Это можно сделать по аксиоме 1.1. Вторая пара точек также определяет прямую. Обозначим ее b. Прямые a и b – разные прямые, потому, что прямая b содержит точку A, которая не принадлежит прямой a. Таким образом, исходя из данных свойств прямой, мы путем рассуждений смогли сделать вывод, что на плоскости существует не одна прямая. Значит, можно приступить к изучению, например, их взаимного расположения на плоскости.

Говорят, что две прямые не пересекаются, если они не имеют ни одной общей точки. Очевидно, что других случаев не может быть, так как, если бы две прямые имели две общие точки, то они бы совпадали, это следует из того, что по аксиоме 1.2 эти точки определяют одну прямую. Этот вывод можно сформулировать в виде утверждения:

2

Рисунок 1.1.2. Взаимное расположение прямых

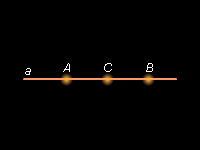
Взаимное положение трех точек A, B, C, лежащих на одной прямой.

На рис. 1.1.3 представлен чертеж прямой a и трех точек A, B и C, лежащих на ней. Чтобы определить взаимное расположение этих точек, говорят, что точка C лежит между точками A и B. Это же можно сказать иначе: либо точка C разделяет точки A и B, либо точки A и B лежат по разные стороны от точки C, либо – точки C и B (C и A) лежат по одну сторону от точки A(B).

3

Рисунок 1.1.3. Взаимное расположение точек на прямой

Свойство трех точек, лежащих на прямой, задается аксиомой: