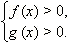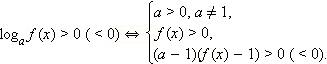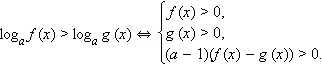Глава 3. Решение уравнений и неравенств
3.2.
3.2.6.
Рассмотрим неравенство 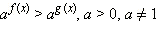 и неравенство, ему равносильное:
и неравенство, ему равносильное:  Для его решения исследуем знак разности
Для его решения исследуем знак разности 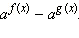 Итак, выясним, что следует из того, что
Итак, выясним, что следует из того, что 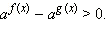
1) Если a > 1, то f (x) > g (x), а это значит, что (a – 1)(f (x) – g (x)) > 0.
2) Если 0 < a < 1, то f (x) < g (x), и опять (a – 1)(f (x) – g (x)) > 0.
Верно и обратное. Если 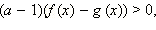 то при
то при 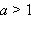 имеем
имеем 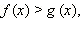 то есть
то есть 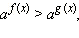 а при
а при 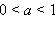 получаем
получаем 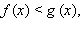 то есть
то есть 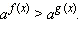
Таким образом, мы доказали, что:
А это как раз обозначает, что получено условие равносильности:

 |
|
Модель 3.4.
Решение показательных неравенств
|
Пример 1Решить неравенство 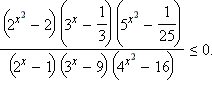
Имеем:
Заменим выражение вида 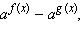
стоящее в каждой скобке, на выражение 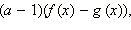
имеющее с ним тот же знак:
А значит, 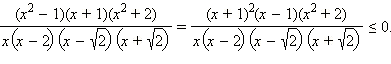 Равносильное неравенство имеет вид
Равносильное неравенство имеет вид 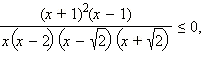 так как
так как 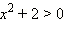 для всех x.
Решая это неравенство методом интервалов, получаем
для всех x.
Решая это неравенство методом интервалов, получаем
Ответ. 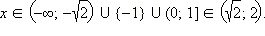
|
Пример 2Решите неравенство 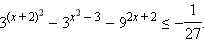
Преобразуем неравенство:
От выражений вида 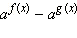 перейдём к выражениям
перейдём к выражениям 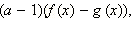 которые имеют тот же знак.
которые имеют тот же знак.
Ответ. 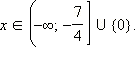
|
Рассмотрим теперь неравенство 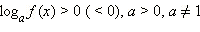 и найдём соответствующие ему условия равносильности. ОДЗ этого неравенства: f (x) > 0.
и найдём соответствующие ему условия равносильности. ОДЗ этого неравенства: f (x) > 0.
Если a > 1, то 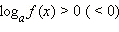 тогда и только тогда, когда f (x) > 1 в ОДЗ (f (x) < 1), то есть
тогда и только тогда, когда f (x) > 1 в ОДЗ (f (x) < 1), то есть 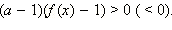
Если 0 < a < 1, то 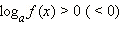 тогда и только тогда, когда f (x) < 1 в ОДЗ (f (x) > 1), то есть опять
тогда и только тогда, когда f (x) < 1 в ОДЗ (f (x) > 1), то есть опять 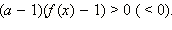
Верно и обратное, если 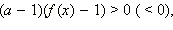 то при a > 1 имеем f (x) > 1 в ОДЗ (f (x) < 1), а при 0 < a < 1 имеем f (x) < 1 в ОДЗ (f (x) > 1). Таким образом, получаем следующие условия равносильности.
то при a > 1 имеем f (x) > 1 в ОДЗ (f (x) < 1), а при 0 < a < 1 имеем f (x) < 1 в ОДЗ (f (x) > 1). Таким образом, получаем следующие условия равносильности.
Отсюда следует, что:
Рассмотрим теперь неравенство вида 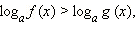 где
где 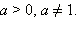 ОДЗ этого неравенства:
ОДЗ этого неравенства: 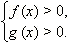
Перепишем данное неравенство в виде:
С учетом ОДЗ можно записать соответствующую неравенству систему уравнений:
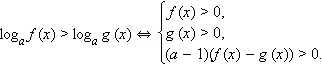

 |
|
Модель 3.2.
Решение логарифмических неравенств
|
Пример 3Решите неравенство 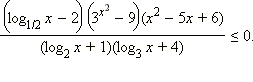
Преобразуем неравенство.
От выражений вида 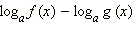 перейдём к произведениям
перейдём к произведениям 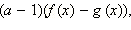 которые имеют с ними тот же знак в ОДЗ.
которые имеют с ними тот же знак в ОДЗ.
Пользуясь методом интервалов, легко получить:
Ответ. 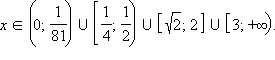
|
Пример 4Решите неравенство
Перейдём во всех логарифмах к основанию 2.
Переходя к равносильной системе, заменим разность логарифмов в фигурных скобках на выражение, которое имеет с ним тот же знак в ОДЗ. Кроме того, заменим логарифм, стоящий до фигурной скобки, на выражение, с которым он совпадает по знаку в ОДЗ.
Так как в ОДЗ 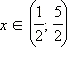 выполнено неравенство
выполнено неравенство 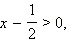 то
то
С учётом сделанного замечания, последняя система в ОДЗ равносильна следующему уравнению:
Так как в ОДЗ x > 0, то знак выражения 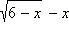 совпадает со знаком функции совпадает со знаком функции 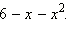
Нанесем решения всех неравенств на числовую прямую и найдем пересечение полученных областей с ОДЗ. Получим:
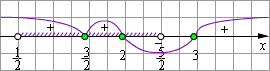 1 1
|
|
Ответ. 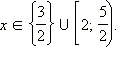
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


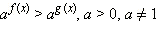 и неравенство, ему равносильное:
и неравенство, ему равносильное:  Для его решения исследуем знак разности
Для его решения исследуем знак разности 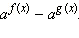 Итак, выясним, что следует из того, что
Итак, выясним, что следует из того, что 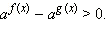
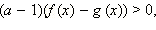 то при
то при 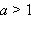 имеем
имеем 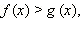 то есть
то есть 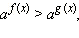 а при
а при 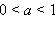 получаем
получаем 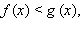 то есть
то есть 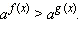
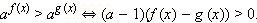


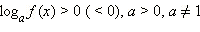 и найдём соответствующие ему условия равносильности. ОДЗ этого неравенства:
и найдём соответствующие ему условия равносильности. ОДЗ этого неравенства: 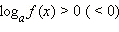 тогда и только тогда, когда
тогда и только тогда, когда 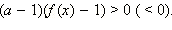
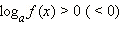 тогда и только тогда, когда
тогда и только тогда, когда 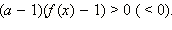
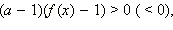 то при
то при 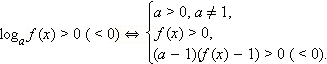
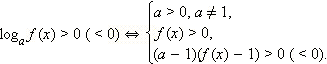
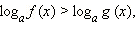 где
где 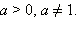 ОДЗ этого неравенства:
ОДЗ этого неравенства: