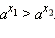Глава 2. Алгебраические выражения
2.2.
2.2.4.
Понятие нецелой степени отрицательного числа не имеет смысла.
Пример 1Вычислить 1) 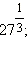 2)
2) 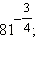 3)
3) 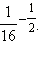
1) 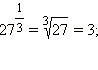
2) 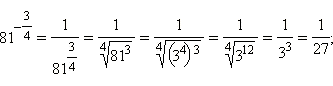
3) 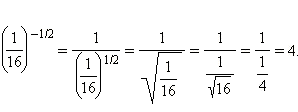
Ответ. 1) 3; 2) 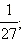 3) 4.
3) 4.
|
Пример 2Упростите выражения 1) 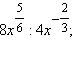 2)
2) 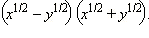
1) 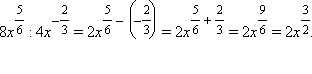
2) 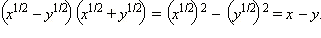
Ответ. 1) 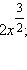 2) x – y.
2) x – y.
|
Итак, для любого действительного числа мы определили операцию возведения в натуральную степень; для любого числа 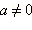 мы определили возведения в нулевую и целую отрицательную степень; для любого
мы определили возведения в нулевую и целую отрицательную степень; для любого 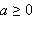 мы определили операцию возведения в положительную дробную степень; для любого
мы определили операцию возведения в положительную дробную степень; для любого 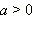 мы определили операцию возведения в отрицательную дробную степень.
мы определили операцию возведения в отрицательную дробную степень.
Возникает естественный вопрос: можно ли каким-либо образом определить операцию возведения в иррациональную степень, а, следовательно, определить смысл выражения ax и для любого действительного числа x? Оказывается, что для положительных чисел a можно придать смысл записи aα , где α − иррациональное число. Для этого нужно рассмотреть три случая: a = 1, a > 1, 0 < a < 1.
- Если a = 1, то по определению полагают, что 1α = 1.
- Если a > 1, то выберем любое рациональное число r1 < α и любое рациональное число r2 > α. Тогда, очевидно, r1 < r2 и, следовательно:
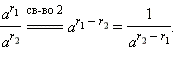
Но
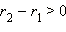 и потому (так как a > 1)
и потому (так как a > 1)
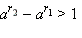 и, наконец,
и, наконец,
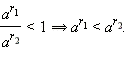
Под 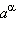 понимают такое число, которое лежит между
понимают такое число, которое лежит между 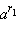 и
и 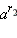 при любом выборе чисел
при любом выборе чисел 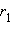 и
и 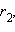 обладающих свойством
обладающих свойством 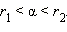 Можно доказать, что число
Можно доказать, что число 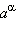 существует и единственно для любого a > 1 и любого иррационального α.
существует и единственно для любого a > 1 и любого иррационального α.
- Если 0 < a < 1, то выберем любое рациональное число
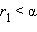 и любое рациональное число
и любое рациональное число 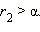 Тогда, очевидно,
Тогда, очевидно, 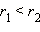 и, следовательно,
и, следовательно, 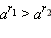 (это неравенство доказывается аналогично приведённому выше для a > 1). Под
(это неравенство доказывается аналогично приведённому выше для a > 1). Под 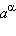 понимают такое число, которое лежит между
понимают такое число, которое лежит между 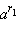 и
и 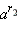 при любом выборе чисел
при любом выборе чисел 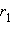 и
и 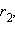 обладающих свойством
обладающих свойством 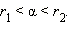 Можно доказать, что число
Можно доказать, что число 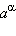 существует и единственно для любого 0 < a < 1 и любого иррационального α.
существует и единственно для любого 0 < a < 1 и любого иррационального α.
Итак, для a > 0 мы определили степень с любым действительным показателем.
Выше мы определили значение выражения ab для всех вещественных a > 0 и всех вещественных b. Теперь мы можем определить степенную функцию.
Заметим, что для натуральных a степенная функция определена на всей числовой оси, подробнее об этом см. курс «Открытая Математика 2.6. Функции и Графики», § 2.4.2. Для произвольных вещественных a это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x.
К основным свойствам степенной функции y = xa при a > 0 относятся:
- Область определения функции − промежуток (0; +∞).
- Область значений функции − промежуток (0; +∞).
- Для любых a график функции проходит через точку (1; 1).
- Функция строго монотонно возрастает на всей числовой прямой, то есть, если
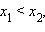 то
то 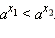
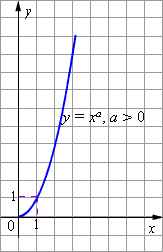
- График степенной функции при a > 0 изображён на рисунке.
 1 1
|
| Рисунок 2.2.4.1. Степенная функция y = xa при a > 0 |
 2 2
|
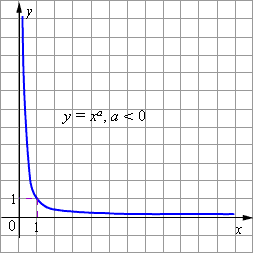
| Рисунок 2.2.4.2. Степенная функция y = xa при a < 0 |
К основным свойствам степенной функции y = xa при a < 0 относятся:
- Область определения функции − промежуток (0; +∞).
- Область значений функции − промежуток (0; +∞).
- Для любых a график функции проходит через точку (1; 1).
- Функция строго монотонно убывает на всей числовой прямой, то есть если
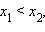 то
то 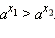
- График степенной функции при a < 0 изображён на рисунке.


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".






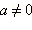 мы определили возведения в нулевую и целую отрицательную степень; для любого
мы определили возведения в нулевую и целую отрицательную степень; для любого 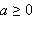 мы определили операцию возведения в положительную дробную степень; для любого
мы определили операцию возведения в положительную дробную степень; для любого 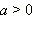 мы определили операцию возведения в отрицательную дробную степень.
мы определили операцию возведения в отрицательную дробную степень. 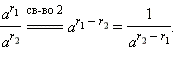
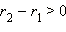 и потому (так как
и потому (так как 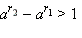 и, наконец,
и, наконец,
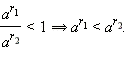
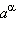 понимают такое число, которое лежит между
понимают такое число, которое лежит между 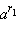 и
и 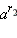 при любом выборе чисел
при любом выборе чисел 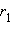 и
и 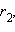 обладающих свойством
обладающих свойством 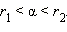 Можно доказать, что число
Можно доказать, что число 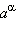 существует и единственно для любого
существует и единственно для любого 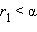 и любое рациональное число
и любое рациональное число 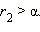 Тогда, очевидно,
Тогда, очевидно, 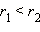 и, следовательно,
и, следовательно, 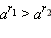 (это неравенство доказывается аналогично приведённому выше для
(это неравенство доказывается аналогично приведённому выше для 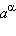 понимают такое число, которое лежит между
понимают такое число, которое лежит между 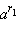 и
и 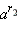 при любом выборе чисел
при любом выборе чисел 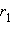 и
и 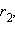 обладающих свойством
обладающих свойством 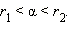 Можно доказать, что число
Можно доказать, что число 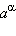 существует и единственно для любого
существует и единственно для любого 



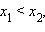 то
то 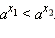


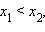 то
то