Учебник. События и вероятности

Все задачи курса теории вероятностей связаны с многократным повторением испытаний и фиксацией результата испытаний – событий. Рассмотрим различные события на примере бросков игрального кубика – A. Будем обозначать тот факт, что на кубике выпало некоторое число от 1 до 6, буквой A с индексом, обозначающим выпавшее число. Так, A₃ обозначает, что при броске кубика A выпало число 3.

• В нашем случае события A₁, A₂, A₃, A₄, A₅, A₆ образуют множество элементарных событий. Для них верно $\sum _i{p}_i=1\mathrm{.}$

  Для бросков кубика класс элементарных событий может быть выбран и так: событие C₁ заключается в том, что выпала грань с чётным количеством очков, C₂ – с нечётным. Тогда p (C₁) + p (C₂) = 1. А вот класс, состоящий из событий «выпало чётное количество очков», «выпала единица», «выпала двойка», «выпала тройка», не является элементарным, хотя для них $\sum _i{p}_i=1\mathrm{.}$ Это связано с тем, что событие «выпало 2» относится сразу к двум событиям этого класса: «выпало чётное количество очков» и «выпала двойка».

• К классу возможных событий относятся все подмножества множества элементарных событий. Например, при броске «выпало 1 или 2», «выпало 3» и т. д.

• Невозможное событие (O) определяется как событие, не входящее в класс возможных. В нашем случае это, например, «не выпало ничего» или «на кубике A выпало число 7». Вероятность невозможного события равна p (O) = 0.

• Достоверное событие (I): случилось хотя бы одно событие из класса возможных. В нашем случае достоверно то, что на каждом из кубиков A и B выпадет любое число от 1 до 6. Вероятность достоверного события равна p (I) = 1.

• Событие, противоположное событию A, обозначается как $\overline{A}$ и состоит в том, что в результате испытания A не произошло. Например, в нашем случае ${\overline{A}}_1$ значит, что на кубике A выпало число, не равное 1.

  Сумма вероятностей события и его отрицания есть достоверное событие, то есть $p\mathrm{(}A\mathrm{)}+p\mathrm{(}\overline{A}\mathrm{)}=1$

  Выпишем все возможные результаты броска кубика A: A₁, A₂, A₃, A₄, A₅, A₆. В этом случае общее число равновероятных вариантов N = 6, при этом $A_1$ встречается $N\mathrm{(}{A}_1\mathrm{)}=1$ раз, «не 1» – $N\mathrm{(}{\overline{A}}_1\mathrm{)}=5\text{ раз}$ Значит, $p\mathrm{(}{A}_1\mathrm{)}=1/6\mathrm{,}$  $p\mathrm{(}{\overline{A}}_1\mathrm{)}=5/6$ $p\mathrm{(}A\mathrm{)}+p\mathrm{(}\overline{A}\mathrm{)}=1$

  Вообще, поскольку все возможные варианты заключаются либо в событии A, либо в событии «не A», то $p\mathrm{(}A\mathrm{)}+p\mathrm{(}\overline{A}\mathrm{)}=\frac{N\mathrm{(}A\mathrm{)}}{N}+\frac{N\mathrm{(}\overline{A}\mathrm{)}}{N}=\frac{N\mathrm{(}A\mathrm{)}}{N}+\frac{N-N\mathrm{(}A\mathrm{)}}{N}=1$

• Несовместными называются события, которые не могут произойти одновременно. Например, события A₁ и A₂ являются несовместными: на кубике A не могут одновременно выпасть 1 и 2.

• Суммой событий A и B называется событие, при котором произошло или A, или B, обозначается оно A + B. Например, A₁ + A₅ означает, что на кубике A выпало или 1, или 5. Можно доказать, что вероятности несовместных событий складываются, то есть, если бросать только кубик A, то p (A₁ + A₅) = p (A₁) + p (A₅) = 1/6 + 1/6 = 1/3.

  Выпишем все возможные результаты броска кубика A: A₁, A₂, A₃, A₄, A₅, A₆. Действительно, вариантов с выпадением 1 или 5 два, всего вариантов шесть, получаем p (A₁ + A₅) = 2/6 = 1/3.

  Пусть из N возможных исходов a вариантов приводят к событию A, b вариантов – к событию B, причём A и B несовместны. Тогда $p\mathrm{(}A+B\mathrm{)}=\frac{a+b}{N}=\frac{a}{N}+\frac{b}{N}=p\mathrm{(}A\mathrm{)}+p\mathrm{(}B\mathrm{)}$

Если бросать одновременно два кубика A и B, то событием будет пара чисел (a, b), выпавших на кубиках A и B соответственно. Обозначим это событие A_aB_b. Например, A₁B₅ означает, что мы бросили два кубика одновременно, на кубике A выпало 1, а на B выпало 5.

• Произведением событий A и B называется событие, при котором произошло и A, и B, обозначается оно AB.

• Независимыми называются события A и B, если вероятность события A не зависит от того, наступило событие B или нет. Например, при броске двух кубиков A₁ и B₅ – независимые события. Вероятность произведения независимых событий равна произведению соответствующих вероятностей. Вообще, равенство p (A_iA_k) = p(A_i) p(A_k) является определением независимых событий.

  При бросании кубика A может наступить 6 различных исходов, а при бросании кубика B – тоже 6. Из комбинаторики мы знаем, что количество вариантов, возникающих при бросании двух кубиков (A₁B₁, A₁B₂ и так далее), равно произведению количества исходов для кубиков A и B в отдельности, то есть 6 ċ 6 = 36. Поскольку все такие исходы равновероятны, то каждый из них может наступить с вероятностью 1/36.

  В нашем случае p (A₁B₅) = p (A₁) p (B₅) = 1/6 ċ 1/6 = 1/36.

• Если вероятность наступления события A зависит от того, наступило событие B или нет, события называют зависимыми и вводят понятие условной вероятности. Условной вероятностью события A при условии того, что произошло событие B, называют величину $\mathrm{p }\mathrm{(}A|B\mathrm{)}=\frac{\mathrm{p }\mathrm{(}AB\mathrm{)}}{\mathrm{p }\mathrm{(}B\mathrm{)}}$ . Соответственно, для зависимых событий p (AB) = p (B) p (A | B).

Теперь, ознакомившись с языком теории вероятностей, мы можем дать более строгое определение вероятности и выписать основные её свойства.

Вероятностью события p(A) называется некоторая действительная функция, определённая на классе возможных событий E и удовлетворяющая следующим трём аксиомам, сформулированным А. Н. Колмогоровым.

Из перечисленных аксиом можно вывести следующие свойства вероятностей.

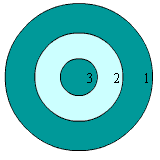
Пусть для некоторого стрелка вероятность попадания в область 1 мишени, изображённой на рисунке, равна 0,25, а вероятность попадания в область 2 – 0,15. Какова вероятность того, что стрелок попадёт либо в область 1, либо в область 2?

По правилу сложения вероятностей получаем, что искомая вероятность

P = 0,25 + 0,15 = 0,4.

Ответ. 0,4.