Глава 9. Координаты и векторы в пространстве

Модель 9.2.  Векторное произведение

Рассмотрим два произвольных вектора: 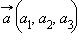и 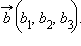  Векторным произведением вектора 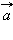на вектор 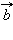называется третий вектор 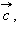который обладает следующими свойствами:

• Его длина равна
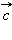• Вектор перпендикулярен к плоскости, в которой лежат вектора и
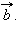
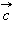• Вектор направлен так, что поворот от вектора 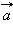к вектору 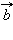осуществляется против часовой стрелки, если смотреть из конца вектора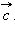

Векторное произведение обозначается квадратными скобками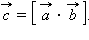

Свойства векторного произведения:

• векторное произведение произвольного вектора на нулевой вектор, равно нулевому вектору;
• векторное произведение двух коллинеарных векторов равно нулевому вектору;
• координаты векторного произведения 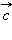векторов 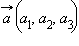и 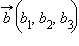следующие: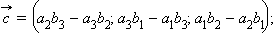
• 

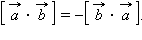
При помощи полей численного ввода можно изменить координаты векторов 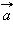и 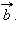В окне вывода будут показаны координаты вектора 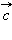и его длина.

Переключившись в демонстрационный режим при помощи кнопки со значком кинопроектора, можно просмотреть анимацию. Кнопка Старт запускает ее, кнопка Стоп – приостанавливает, а кнопка Сброс возвращает анимацию в исходное состояние. Кнопка со значком руки переводит модель обратно в интерактивный режим.