Глава 9. Координаты и векторы в пространстве

Модель 9.3.  Уравнение плоскости в пространстве

Общее уравнение плоскости в декартовой системе координат записывается следующим образом:

ax + by + cz + d = 0.

Если известно, что плоскость проходит через точку с координатами (x₀, y₀, z₀), то ее уравнение можно привести к виду

a (x – x0) + b (y – y0) + c (z – z0) = 0.

Уравнение
называется уравнением плоскости в отрезках на осях.

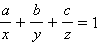Нормаль к плоскости имеет координаты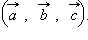

Угол между двумя плоскостями легко вычисляется по формуле скалярного произведения. Если эти плоскости задаются уравнениями a₁x + b₁y + c₁z + d₁ = 0 и a₂x + b₂y + c₂z + d₂ = 0, то угол между плоскостями равняется

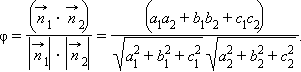Расстояние от точки (x₀; y₀; z₀) до плоскости, задаваемой уравнением ax + by + cz + d = 0, равно

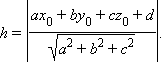В интерактивном режиме можно выбрать опции Плоскость и точка или Две плоскости. В первой опции пользователю демонстрируется расстояние от точки до плоскости. Указанное расстояние и уравнения плоскости в различном виде можно увидеть в окне вывода. Во второй опции показывается угол между двумя плоскостями.

Переключившись в демонстрационный режим при помощи кнопки со значком кинопроектора, можно просмотреть анимацию. Кнопка Старт запускает ее, кнопка Стоп – приостанавливает, а кнопка Сброс возвращает анимацию в исходное состояние. Кнопка со значком руки переводит модель обратно в интерактивный режим.