 Модель 9.4.
Уравнение прямой в пространстве
Модель 9.4.
Уравнение прямой в пространстве |
Уравнение прямой в трехмерной декартовой системе координат, параллельной вектору
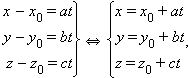 |
Вектор
Угол между двумя прямыми вычисляется по формуле скалярного произведения. Если эти прямые параллельны векторам
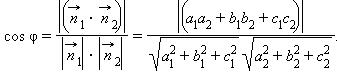 |
Введите координаты направляющих векторов обеих прямых, а также координаты точки их пересечения. В окне вывода будут показаны уравнения прямых и угол между ними.
Переключившись в демонстрационный режим при помощи кнопки со значком кинопроектора, можно просмотреть анимацию. Кнопка запускает ее, кнопка – приостанавливает, а кнопка возвращает анимацию в исходное состояние. Кнопка со значком руки переводит модель обратно в интерактивный режим.


