Глава 5. Тела вращения

5.7. Поверхности второго порядка

К невырожденным поверхностям второго порядка относятся эллипсоид, эллиптический параболоид, гиперболический параболоид, однополостной гиперболоид и двуполостной гиперболоид. Строгое изучение этих поверхностей проводится в курсе аналитической геометрии. Здесь же мы ограничимся определениями и иллюстрациями.

Определение 5.12. 

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением 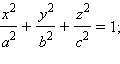 a > 0, b > 0, c > 0, называется эллипсоидом.

1

Рисунок 5.7.1

Свойства эллипсоида.

1. Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что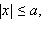   

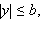
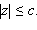
2. Эллипсоид обладает

   • центральной симметрией относительно начала координат,
   • осевой симметрией относительно координатных осей,
   • плоскостной симметрией относительно начала координат.

3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.

2

Рисунок 5.7.2

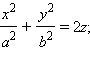
Свойства эллиптического параболоида.

1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.

2. Эллиптический параболоид обладает

   • осевой симметрией относительно оси Oz,
   • плоскостной симметрией относительно координатных осей Oxz и Oyz.

3. В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – парабола.

3

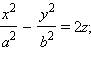
Рисунок 5.7.3

Свойства гиперболического параболоида.

1. Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2. Гиперболический параболоид обладает

   • осевой симметрией относительно оси Oz,
   • плоскостной симметрией относительно координатных плоскостей Oxz и Oyz.

3. В сечении гиперболического параболоида плоскостью, ортогональной оси координат Oz, получается гипербола, а плоскостями, ортогональными осям Ox и Oy, – парабола.

4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.

4

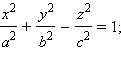
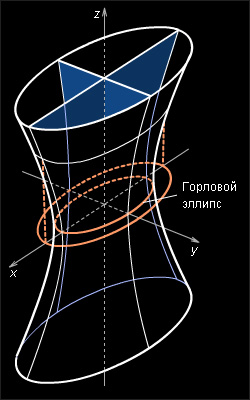
Рисунок 5.7.4

Свойства однополостного гиперболоида.

1. Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2. Однополостной гиперболоид обладает

   • центральной симметрией относительно начала координат,
   • осевой симметрией относительно всех координатных осей,
   • плоскостной симметрией относительно всех координатных плоскостей.

3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.

5

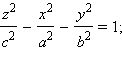
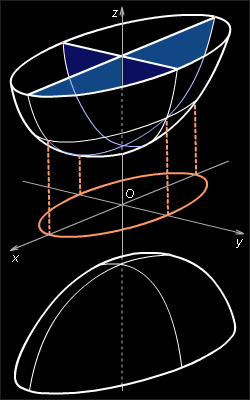
Рисунок 5.7.5

Свойства двуполостного гиперболоида.

1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что 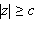и неограничен сверху.

2. Двуполостный гиперболоид обладает

   • центральной симметрией относительно начала координат,
   • осевой симметрией относительно всех координатных осей,
   • плоскостной симметрией относительно всех координатных плоскостей.

3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 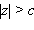Oz, при получается эллипс, при 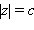– точка, а в сечении плоскостями, перпендикулярными осям Ox и Oy, – гипербола.

По аналогии с коническими сечениями существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x² = 0 описывается пара совпадающих плоскостей, уравнением x² = 1 – пара параллельных плоскостей, уравнением x² – y² = 0 – пара пересекающихся плоскостей. Уравнение x² + y² + z² = 0 описывает точку с координатами (0; 0; 0), уравнение x² + y² = 1 – круговой цилиндр, уравнение x² + y² = z² – круговой конус. Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии.