Глава 5. Решение треугольников

Модель 5.3.  Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:

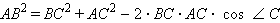Это утверждение, называемое теоремой косинусов, и демонстрируется в интерактивной модели. В треугольнике ABC можно перетаскивать мышью точки B и C. Показываются длины сторон треугольника, градусные меры углов. При помощи группы переключателей можно выбрать какую-либо сторону треугольника; в окне вывода появятся значения всех элементов, имеющихся в теореме косинусов. Убедитесь, что эта теорема выполняется как в тупоугольных, так и в остроугольных треугольниках.

Переключившись в демонстрационный режим при помощи кнопки со значком кинопроектора, можно просмотреть анимацию. Кнопка Старт запускает ее, кнопка Стоп – приостанавливает, а кнопка Сброс возвращает анимацию в исходное состояние. Кнопка со значком руки переводит модель обратно в интерактивный режим.