Глава 1. Точка и прямая

Модель 1.1.  Длина отрезка

По одной из основных аксиом планиметрии, каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин его частей, на которые он разбивается любой своей внутренней точкой.

Интерактивная модель демонстрирует понятие длины отрезка. В центральном окне можно увидеть отрезок AB, одна из точек которого – B – не зафиксирована; ее можно, захватив мышью, перемещать по горизонтали влево-вправо. Между точками A и B по отрезку можно также перемещать точку C при помощи мыши. Эта точка делит отрезок AB на две части, причем, согласно аксиоме, AB = AC + BC. Специальный выключатель Показать длины выводит на экран длины всех отрезков. Убедитесь, что независимо от расположения на отрезке AB точки C, приведенная аксиома выполняется во всех случаях. Выберите переключатель Неравенство треугольника. Теперь точку C можно перемещать на плоскости при помощи мыши где угодно. Убедитесь, что в получившемся треугольнике ABC при любых положениях точек B и C выполняется теорема о неравенстве треугольника: Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки:

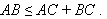Переключившись в демонстрационный режим при помощи кнопки со значком кинопроектора, можно просмотреть анимацию. Кнопка Старт запускает ее, кнопка Стоп – приостанавливает, а кнопка Сброс возвращает анимацию в исходное состояние. Кнопка со значком руки переводит модель обратно в интерактивный режим.