Глава 10. Декартовы координаты

Модель 10.4.
Линии второго порядка
Линии, задаваемые на координатной плоскости уравнениями второго порядка, называются фигурами второго порядка. К ним относятся эллипс, парабола, гипербола, а также вырожденные случаи (прямая, пара прямых, точка, пустое множество).
Эллипс задается каноническим уравнением 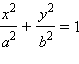 . Эта фигура пересекает каждую из осей координат в двух точках и симметрична относительно начала координат и координатных осей. Эллипс является геометрическим местом точек, сумма расстояний от которых до двух заданных точек (фокусов эллипса) постоянна. Это означает, что эллипс можно построить при помощи натянутой нити следующим образом. Если концы нити заданной длины закреплены в точках F1 и F2, то кривая, описываемая острием карандаша, скользящим по туго натянутой нити, имеет форму эллипса. Заметим, что координаты фокусов эллипса равняются
. Эта фигура пересекает каждую из осей координат в двух точках и симметрична относительно начала координат и координатных осей. Эллипс является геометрическим местом точек, сумма расстояний от которых до двух заданных точек (фокусов эллипса) постоянна. Это означает, что эллипс можно построить при помощи натянутой нити следующим образом. Если концы нити заданной длины закреплены в точках F1 и F2, то кривая, описываемая острием карандаша, скользящим по туго натянутой нити, имеет форму эллипса. Заметим, что координаты фокусов эллипса равняются 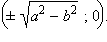 Если точки
Если точки 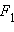 и
и 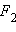 совпадают (т.е. a = b), то эллипс превращается в окружность; эллипс можно получить из окружности сжатием ее к оси y в
совпадают (т.е. a = b), то эллипс превращается в окружность; эллипс можно получить из окружности сжатием ее к оси y в 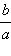 раз.
раз.
Параболу можно задать каноническим уравнением y2 = 2px. Эта фигура симметрична относительно оси Ox. Парабола имеет единственный фокус с координатами 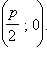 Парабола является геометрическим местом точек, равноудаленных от фокуса и заданной прямой – директрисы параболы. Для построения параболы нужно расположить линейку так, чтобы ее край совпал с директрисой, и приложить к этому краю катет AC чертежного треугольника ABC. Закрепим один конец нити длиной AB в вершине B треугольника, а другой – в фокусе параболы F. Натянув острием карандаша нить, прижмем острие в переменной точке P к свободному катету AB чертежного треугольника. По мере того, как треугольник будет перемещаться вдоль линейки, точка P будет описывать дугу параболы с фокусом F и директрисой.
Парабола является геометрическим местом точек, равноудаленных от фокуса и заданной прямой – директрисы параболы. Для построения параболы нужно расположить линейку так, чтобы ее край совпал с директрисой, и приложить к этому краю катет AC чертежного треугольника ABC. Закрепим один конец нити длиной AB в вершине B треугольника, а другой – в фокусе параболы F. Натянув острием карандаша нить, прижмем острие в переменной точке P к свободному катету AB чертежного треугольника. По мере того, как треугольник будет перемещаться вдоль линейки, точка P будет описывать дугу параболы с фокусом F и директрисой.
Гипербола задается каноническим уравнением 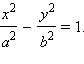 Гипербола не имеет общих точек с осью Oy, а с осью Ox пересекается в двух точках (±a; 0). Гипербола имеет две перпендикулярные оси симметрии и центр симметрии. Фокусы гиперболы расположены в точках
Гипербола не имеет общих точек с осью Oy, а с осью Ox пересекается в двух точках (±a; 0). Гипербола имеет две перпендикулярные оси симметрии и центр симметрии. Фокусы гиперболы расположены в точках 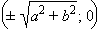 . При построении гиперболы точка P, острие карандаша, фиксируется на нити, которая свободно скользит по шпенькам, установленным в фокусах F1 и F2. Расстояния подобраны так, что отрезок PF2 превосходит по длине отрезок PF1 на фиксированную величину, меньшую расстояния F1F2. При этом один конец нити проходит под шпеньком F1, и оба конца нити проходят поверх шпенька F2. Острие карандаша не должно скользить по нити, поэтому его нужно закрепить, сделав на нити маленькую петлю и продев в нее острие. Одну ветвь гиперболы (PV1Q) мы вычерчиваем, следя за тем, чтобы нить оставалась все время натянутой, и, потягивая оба конца нити вниз за точку F2, а когда точка P окажется ниже отрезка F1F2, придерживая нить за оба конца и осторожно отпуская ее. Вторую ветвь гиперболы P'V2Q' мы вычерчиваем, предварительно поменяв ролями шпеньки F1 и F2.
. При построении гиперболы точка P, острие карандаша, фиксируется на нити, которая свободно скользит по шпенькам, установленным в фокусах F1 и F2. Расстояния подобраны так, что отрезок PF2 превосходит по длине отрезок PF1 на фиксированную величину, меньшую расстояния F1F2. При этом один конец нити проходит под шпеньком F1, и оба конца нити проходят поверх шпенька F2. Острие карандаша не должно скользить по нити, поэтому его нужно закрепить, сделав на нити маленькую петлю и продев в нее острие. Одну ветвь гиперболы (PV1Q) мы вычерчиваем, следя за тем, чтобы нить оставалась все время натянутой, и, потягивая оба конца нити вниз за точку F2, а когда точка P окажется ниже отрезка F1F2, придерживая нить за оба конца и осторожно отпуская ее. Вторую ветвь гиперболы P'V2Q' мы вычерчиваем, предварительно поменяв ролями шпеньки F1 и F2.
В интерактивном режиме при помощи полей числового ввода можно изменять параметры фигур второго порядка (a, b, p). Наблюдайте, как изменяется внешний вид фигуры на экране, а также расположение ее фокусов и директрисы.
Переключившись в демонстрационный режим при помощи кнопки со значком кинопроектора, можно просмотреть анимацию. Кнопка запускает ее, кнопка – приостанавливает, а кнопка возвращает анимацию в исходное состояние. Кнопка со значком руки переводит модель обратно в интерактивный режим.



Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".
 Модель 10.4.
Линии второго порядка
Модель 10.4.
Линии второго порядка
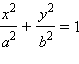 . Эта фигура пересекает каждую из осей координат в двух точках и симметрична относительно начала координат и координатных осей. Эллипс является геометрическим местом точек, сумма расстояний от которых до двух заданных точек (фокусов эллипса) постоянна. Это означает, что эллипс можно построить при помощи натянутой нити следующим образом. Если концы нити заданной длины закреплены в точках
. Эта фигура пересекает каждую из осей координат в двух точках и симметрична относительно начала координат и координатных осей. Эллипс является геометрическим местом точек, сумма расстояний от которых до двух заданных точек (фокусов эллипса) постоянна. Это означает, что эллипс можно построить при помощи натянутой нити следующим образом. Если концы нити заданной длины закреплены в точках 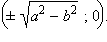 Если точки
Если точки 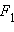 и
и 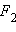 совпадают (т.е.
совпадают (т.е. 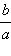 раз.
раз.
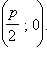 Парабола является геометрическим местом точек, равноудаленных от фокуса и заданной прямой – директрисы параболы. Для построения параболы нужно расположить линейку так, чтобы ее край совпал с директрисой, и приложить к этому краю катет
Парабола является геометрическим местом точек, равноудаленных от фокуса и заданной прямой – директрисы параболы. Для построения параболы нужно расположить линейку так, чтобы ее край совпал с директрисой, и приложить к этому краю катет 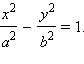 Гипербола не имеет общих точек с осью
Гипербола не имеет общих точек с осью 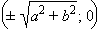 . При построении гиперболы точка
. При построении гиперболы точка 

