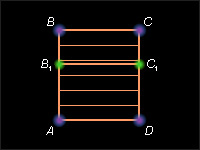
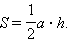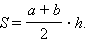Пусть ABCD и AB₁C₁D – два прямоугольника с общим основанием AD (рис. 13.2.1).

1 Рисунок 13.2.1. К теореме 13.2

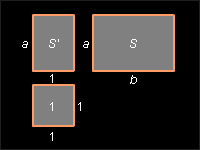2 Рисунок 13.2.2. К теореме 13.2

Пусть S и 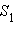– их площади. Докажем, что 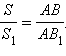  Разобьем сторону AB прямоугольника на некоторое число n равных частей, каждая из которых равна 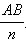  Пусть m – число точек деления, которые лежат нa стороне AB₁. Тогда 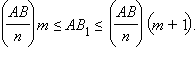  Отсюда, разделив на AB, получим

(*)

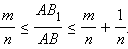Проведем через точки деления прямые, параллельные основанию AD. Они разобьют прямоугольник ABCD на n равных прямоугольников. Каждый из них имеет площадь 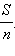  Прямоугольник 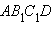содержит первые m прямоугольника, считая от стороны AD, и содержится в m + 1 прямоугольниках. Поэтому 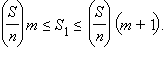  Отсюда   (**)

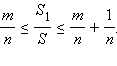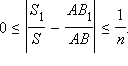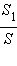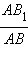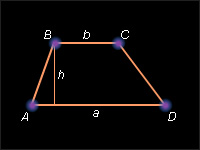
Сравнивая неравенства (*) и (**), заключаем, что   При этом   и  – фиксированные числа, а n может быть выбрано сколь угодно большим. Следовательно, неравенство возможно только при  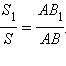 Возьмем теперь единичный квадрат, прямоугольник со сторонами 1, a и прямоугольник со сторонами a, b (рис. 13.2.2). Площадь прямоугольника со сторонами 1 и a обозначим 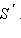Сравнивая их площади, по доказанному будем иметь 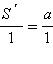  и 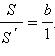  Перемножая эти равенства почленно, получим S = a · b. Теорема доказана.

Пусть ABCD – данный параллелограмм. Если он не является прямоугольником, то один из его углов A или B острый. Пусть для определенности A острый (рис. 13.2.3).

3

Рисунок 13.2.3. К теореме 13.3

Опустим перпендикуляр AE из вершины A на прямую CB. Площадь трапеции AECD равна сумме площадей параллелограмма ABCD и треугольника AEB. Опустим перпендикуляр DF из вершины D на прямую CD. Тогда площадь трапеции AECD равна сумме площадей прямоугольника AEFD и треугольника DFC. Прямоугольные треугольники AEB и DFC равны, а значит, имеют равные площади. Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника AEFD, т.е. равна AE ·  AD. Отрезок AE – высота параллелограмма, соответствующая стороне AD, и, следовательно, S = a · h. Теорема доказана.

Пусть ABC – данный треугольник (рис. 13.2.7). Дополним его до параллелограмма ABCD, как показано на рисунке.

7

Рисунок 13.2.7. К теореме 13.4

Площадь параллелограмма равна сумме площадей треугольников ABC и CDA. Так как эти треугольники равны, то площадь параллелограмма равна удвоенной площади треугольника ABC. Высота параллелограмма, соответствующая стороне CB, равна высоте треугольника, проведенной к стороне CB. Отсюда следует утверждение теоремы, и  Теорема доказана.

Пусть ABCD – данная трапеция (рис. 13.2.9).

9

Рисунок 13.2.9. К теореме 13.5

Диагональ AC трапеции разбивает ее на два треугольника: ABC и CDA. Следовательно, площадь трапеции равна сумме площадей этих треугольников. Площадь треугольника ACD равна   площадь треугольника ABC равна   Высоты AF и CE этих треугольников равны расстоянию h между параллельными прямыми BC и AD, т.е. высоте трапеции. Следовательно,   Теорема доказана.