 |
 |
Определим преобразование точек плоскости следующим образом. Пусть задана окружность 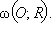 Каждой точке
Каждой точке 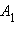 на луче
на луче
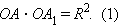 |

Соответствие между точками плоскости, заданное соотношением (1), является взаимно однозначным преобразованием всех точек плоскости, за исключением точки 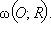
Это преобразование называется преобразованием инверсии или просто инверсией относительно окружности 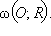 Обозначим ее
Обозначим ее 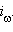 Образ точки
Образ точки
В определении инверсии выражение (1) симметрично относительно сомножителей, что позволяет трактовать точку 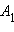 при инверсии
при инверсии 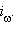 Сформулируем на этой основе следующее свойство инверсии.
Сформулируем на этой основе следующее свойство инверсии.

Если точке  соответствует точка
соответствует точка 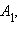 то точке
то точке 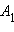 соответствует точка
соответствует точка 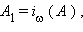 то верно
то верно 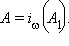
Точки
Очевидно, что если 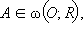 то
то 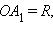 то есть
то есть
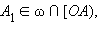 и, следовательно,
и, следовательно, 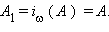

При инверсии относительно 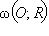 каждая точка окружности
каждая точка окружности
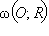 неподвижна.
неподвижна.
В остальных случаях из пары связанных инверсий точек одна лежит внутри окружности
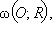 другая – вне этой окружности.
другая – вне этой окружности.
|
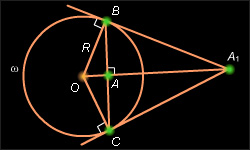
| Рисунок 12.8.1 |
Пусть 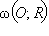 – заданная окружность (рис. 12.8.1). Пусть точка
– заданная окружность (рис. 12.8.1). Пусть точка 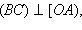 где
где
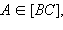
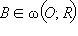 и
и 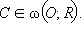 Проведем через точки
Проведем через точки 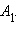 Покажем, что
Покажем, что 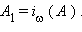
Действительно, из того свойства, что высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому отрезков гипотенузы, полученных разбиением ее основанием высоты, получаем, что 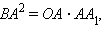 но
но 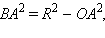 откуда
откуда
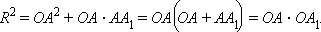 |
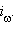

Если две фигуры 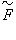 имеют единственную общую точку, то их образы при инверсии также будут иметь единственную общую точку.
имеют единственную общую точку, то их образы при инверсии также будут иметь единственную общую точку.
Введем далее прямоугольную систему координат 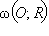 инверсии
инверсии 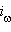 (рис. 12.8.2).
(рис. 12.8.2).
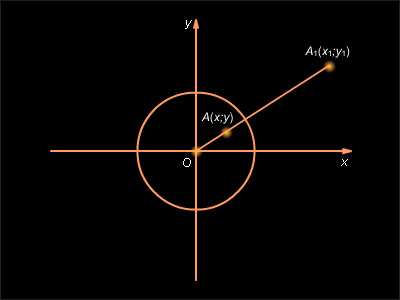
|
| Рисунок 12.8.2 |
Пусть 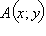 – прообраз точки
– прообраз точки 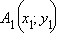 при инверсии
при инверсии 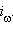 Из рисунка ясно, что
Из рисунка ясно, что  Отсюда имеем
Отсюда имеем
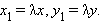 |
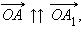 то
то 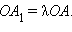 Умножив обе части этого равенства на
Умножив обе части этого равенства на 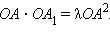 Но, с другой стороны,
Но, с другой стороны, 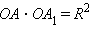 и, кроме того,
и, кроме того, 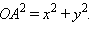 Отсюда имеем
Отсюда имеем
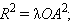 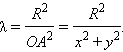 |
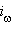 задается соотношениями
задается соотношениями
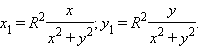 (2) (2)
|
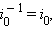 то
то
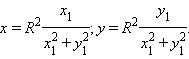 (3) (3)
|

Инверсия преобразует:
Назовем углом между пересекающимися окружностями с вершиной в точке пересечения меньший угол между касательными к ним прямыми в точке пересечения. Аналогично углом между окружностью и пересекающей ее прямой с вершиной в точке пересечения называется угол между этой прямой и касательной к окружности, проведенной в точке пересечения. Из этого определения следует, что если две окружности или прямая и окружность касаются (то есть имеют единственную общую точку), то угол между ними равен нулю.

При инверсии углы сохраняются.

Пусть 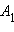 и
и 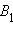 – образы точек
– образы точек 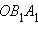 подобны и
подобны и
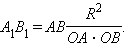 |

Теорема Птолемея. Произведение диагоналей вписанного в окружность четырехугольника равно сумме произведений противоположных его сторон.
 |
 |
 |

