Векторы Задачи с решениями
Задачи с решениями

Найти радиус и координаты центра окружности, проходящей через точку A (–1; 3) и касающейся прямых 7x + y = 0 и x – y + 8 = 0.
Решение
Пусть 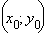 – центр окружности, а R – ее радиус. Тогда уравнение искомой окружности имеет вид
– центр окружности, а R – ее радиус. Тогда уравнение искомой окружности имеет вид 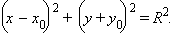
Так как прямая x – y + 8 = 0 касается этой окружности, то система уравнений
имеет единственное решение. Из второго уравнения y = x + 8. Подставив в первое получим
Условие единственности решения – равенство нулю дискриминанта этого уравнения
или
Аналогично анализируем касание окужности со второй прямой 7x + y = 0
С учетом того, что точка A (–1; 3) принадлежит окружности имеем систему из трех уравнений с тремя неизвестными
Из первых двух уравнений имеем 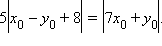 Рассмотрим два возможных случая.
Рассмотрим два возможных случая.
-
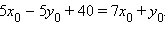 Отсюда
Отсюда 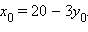 Подставим в последнее уравнение и первое уравнение
Подставим в последнее уравнение и первое уравнение
Система не имеет решений.
-
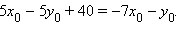 Отсюда
Отсюда 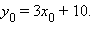 Подставив в первое и третье равенства получим
Подставив в первое и третье равенства получим
a) 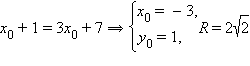 – первое решение.
– первое решение.
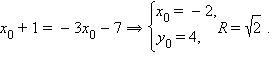 – второе решение.
– второе решение.
 25 из 25
25 из 25
 |
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


 Задачи с решениями
Задачи с решениями

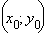 – центр окружности, а
– центр окружности, а 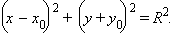
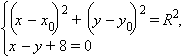
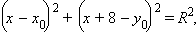
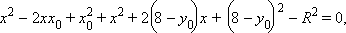
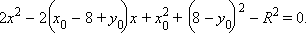
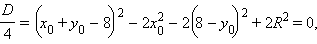
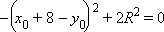
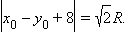
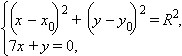
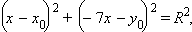
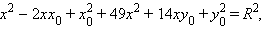
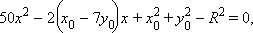
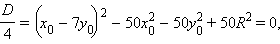
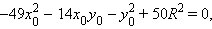
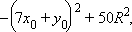
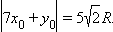
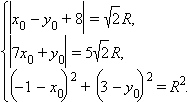
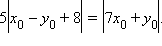 Рассмотрим два возможных случая.
Рассмотрим два возможных случая.
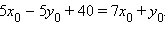 Отсюда
Отсюда 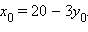 Подставим в последнее уравнение и первое уравнение
Подставим в последнее уравнение и первое уравнение 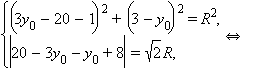
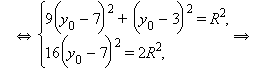
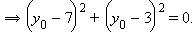
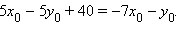 Отсюда
Отсюда 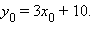 Подставив в первое и третье равенства получим
Подставив в первое и третье равенства получим 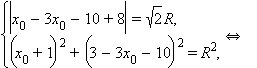
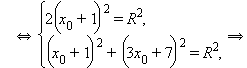
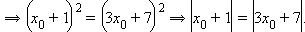
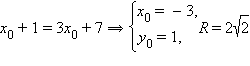 – первое решение.
– первое решение.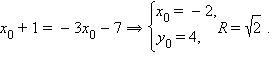 – второе решение.
– второе решение. 25 из 25
25 из 25
