Глава 3. Дифференцирование и интегрирование функций

3.5. Простейшие дифференциальные уравнения

3.5.1. Понятие дифференциального уравнения

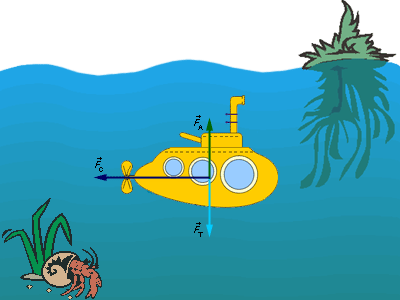
Рассмотрим движение тела массы m в вязкой среде с коэффициентом сопротивления k. По второму закону Ньютона можно записать:

ma = –kv.

Так как ускорение – первая производная скорости,

В это уравнение входит неизвестная величина v и ее производная по времени

1

Рисунок 3.5.1.1. Движение тела в вязкой среде в отсутствие движущей силы

Уравнения, подобные этому, нередко встречаются в физике, химии, экономике и других дисциплинах. Уравнение вида
называется обыкновенным дифференциальным уравнением n-го порядка. Решением этого уравнения является произвольная функция y = y (x), подстановка которой в уравнение превращает его в верное тождество. График решения дифференциального уравнения называется интегральной кривой.

Простейшим дифференциальным уравнением является уравнение вида

Чтобы его решить, нужно представить производную как домножить обе части уравнения на dx и проинтегрировать обе части получившегося уравнения:

Как видно, это уравнение имеет бесконечное количество решений, отличающихся друг от друга на постоянную C. Выбрать конкретное решение уравнения можно, если знать начальные условия, например, точку, через которую проходит график функции y = y (x). Так, если известно, что

y (x0) = y0,

то подставляя это значение в общее решение получаем  откуда и
Это решение можно записать в виде .

Общим решением дифференциального уравнения называется функция y = y (x, C₁, C₂,…, C_n), зависящая от n констант, если она является решением дифференциального уравнения при любых значениях постоянных C₁, C₂,…, C_n.

Неоднозначность общего решения многих уравнений имеет простой физический смысл. Так, дифференциальное уравнение движения материальной точки массы m под действием силы F (второй закон Ньютона)
не определяет однозначно закон движения этой точки: для этого необходимо знать его начальные скорость и координату.

Частным решением дифференциального уравнения называется решение, получаемое из общего решения путем придания определенного значения постоянным C_i.

График 3.5.1.1. Решения уравнения (y')2 + y2 = 1.

2

Рисунок 3.5.1.2. Для исследования решений дифференциального уравнения применяют метод фазовых траекторий. Для этого по осям абсцисс и ординат откладывают, соответственно, саму величину и ее производную. Фазовые траектории могут выглядеть самым причудливым образом даже для линейных дифференциальных уравнений; траектории для уравнения  показаны на графике.

Наряду с частными существуют особые решения, которые нельзя получить из общего решения никакой подстановкой постоянных. Так, общим решением уравнения будет семейство функций y = cos (x + C). Кроме того, это уравнение имеет два особых решения y = 1 и y = –1, в чем можно убедиться подстановкой. Графики особых решений в каждой точке касаются проходящего через эту точку частного решения.

Если задачу об отыскании всех решений дифференциального уравнения удается свести к вычислению конечного числа интегралов и производных от известных функций и к алгебраическим операциям, то говорят, что уравнение интегрируется в квадратурах. К сожалению, класс таких уравнений крайне узок: так, второй закон Ньютона интегрируется только тогда, когда F является функцией только от одной из переменных t, x, Поэтому для исследования дифференциальных уравнений широко применяются приближенные и численные методы.

Во многих случаях приходится составлять дифференциальное уравнение, чтобы решить задачу. Рассмотрим несколько примеров.

1. 3

   Рисунок 3.5.1.3. Реактивное движение.

   Реактивное движение. Ракета, начальная масса которой равна m₀, движется вдали от небесных тел за счет газовой струи, выбрасываемой в направлении, противоположном движению, со скоростью u относительно ракеты. Начальная скорость ракеты равна v₀. Необходимо получить зависимость скорости ракеты от ее массы.

   Запишем закон сохранения импульса. Пусть в некоторый момент времени t импульс ракеты равнялся mv. За бесконечно малый промежуток времени dt скорость ракеты увеличилась от v до v + dv, а масса уменьшилась от m до m – dm, и ракета увеличила свой импульс на выбросив назад dm топлива, импульс которого равен dm (v – u) (здесь и далее уравнение записывается в проекции на ось движения, u > 0). Получаем
   

   Раскрывая скобки и приводя подобные члены, получаем Слагаемое dm · dv бесконечно мало по сравнению с остальными слагаемыми, так как оно является произведением двух бесконечно малых величин; этим слагаемым можно пренебречь. Разделим обе части получившегося уравнения
   на dt:
   

   Это уравнение называется уравнением движения тела с переменной массой. Это дифференциальное уравнение.

2. Истечение идеальной жидкости из сосуда.

   4

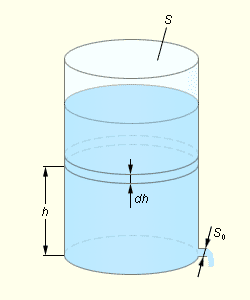
   Рисунок 3.5.1.4. Истечение идеальной жидкости из сосуда

   Пусть из сосуда с постоянной площадью поперечного сечения S через отверстие в дне площадью S₀ вытекает вода. Пренебрегая вязкостью, записать уравнение изменения уровня жидкости в сосуде h.

   Скорость v истечения жидкости из сосуда, уровень жидкости в котором равен h, равна
   (формула Торричелли). За бесконечно малый промежуток времени dt высота жидкости в сосуде уменьшается на dh. Этот же объем S dh истекает через отверстие площадью S₀. Можно записать, что за время dt через отверстие протекает «столб» воды dx = v dt. Таким образом (знак «минус» поставлен из-за того, что уровень воды в сосуде уменьшается). Таким образом,
   Это тоже дифференциальное уравнение.

Модель 3.16. Движение в воздушной среде