Глава 3. Дифференцирование и интегрирование функций
3.3. Неопределенный интеграл
3.3.4. Интегрирование сложных функций
Назовем правильной рациональной дробью функцию вида
 где
где  и
и  – многочлены степеней m и n соответственно, причем m < n. Всякая правильная рациональная дробь раскладывается на сумму простых дробей вида
– многочлены степеней m и n соответственно, причем m < n. Всякая правильная рациональная дробь раскладывается на сумму простых дробей вида
 и и  |
где A, B, D, a, p, q – постоянные 


Любая неправильная дробь
 m ≥ n, представима в виде
m ≥ n, представима в виде
где
 –
правильная дробь, а S (x) – многочлен степени m – n. Для этого можно, например, разделить Pm на Qn «уголком». Так, дробь
–
правильная дробь, а S (x) – многочлен степени m – n. Для этого можно, например, разделить Pm на Qn «уголком». Так, дробь
 не является правильной, для нее получаем:
не является правильной, для нее получаем:
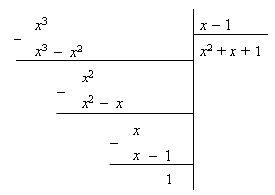
Итак, 
Таким образом, интегралы от дробей вида
 являются степенными или логарифмическими функциями:
являются степенными или логарифмическими функциями:
 (r ≠ 1). (r ≠ 1).
|
Интеграл от дроби вида
 вычисляется методом замены переменного:
вычисляется методом замены переменного:
 где
где
 .
.
При k = 1 эти интегралы соответственно равны
 и
и

При k > 1  а второй интеграл является линейной комбинацией правильной рациональной дроби и арктангенса.
а второй интеграл является линейной комбинацией правильной рациональной дроби и арктангенса.
Некоторые сложные функции интегрируются методом замены переменного.
Так, интеграл вида
 где R (x) – произвольная рациональная функция, сводится к интегралу от рациональной дроби при помощи подстановки
где R (x) – произвольная рациональная функция, сводится к интегралу от рациональной дроби при помощи подстановки
поскольку



Интеграл вида
 где (m + n) – нечетное число, решается подстановкой t = sin x или t = cos x. Если же (m + n) – четное, то используют подстановку t = tg x или t = cos 2x.
где (m + n) – нечетное число, решается подстановкой t = sin x или t = cos x. Если же (m + n) – четное, то используют подстановку t = tg x или t = cos 2x.
Заметим, что некоторые интегралы от трансцендентных функций не выражаются через элементарные функции. К таковым относятся, в частности:
 –
интеграл Пуассона;
–
интеграл Пуассона; и
и
 –
интегралы Френеля;
–
интегралы Френеля; –
интегральный логарифм;
–
интегральный логарифм; –
интегральный синус;
–
интегральный синус; –
интегральный косинус.
–
интегральный косинус.


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".



 и
и  – многочлены степеней
– многочлены степеней  и
и 





 –
–

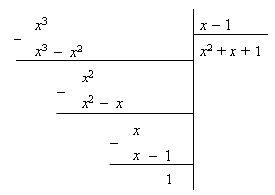






 .
.










 –
–

 –
–
 –
–
 –
–
 –
–




