Геометрический смысл производной Задачи с решениями
Задачи с решениями

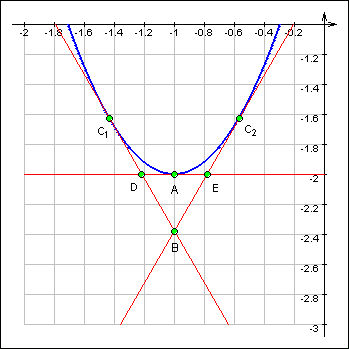
К параболе y = 2x2 + 4x проведены три касательные. Одна из них горизонтальна, а две другие касаются параболы в точках, лежащих по разные стороны от вершины. Треугольник с вершинами в точках пересечения этих касательных является правильным. Найдите площадь этого треугольника.
Решение
Горизонтальная касательная проходит через вершину параболы A (–1; –2). Т.к. график параболы симметричен относительно своей оси, то точка B пересечения наклонных касательных должна лежать на этой оси, а углы наклона этих касательных равны ±60º (

Производная
 откуда
откуда
 (здесь x0 – абсциссы точек касания C1 и C2). Уравнения наклонных касательных имеют вид:
(здесь x0 – абсциссы точек касания C1 и C2). Уравнения наклонных касательных имеют вид:
 Они пересекаются с осью параболы x = –1 в точке
Они пересекаются с осью параболы x = –1 в точке

Длина отрезка
 Длина стороны треугольника
Длина стороны треугольника
 Площадь треугольника BDE равна
Площадь треугольника BDE равна

 4 из 5
4 из 5
 |
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".


 Задачи с решениями
Задачи с решениями









 4 из 5
4 из 5
