Основные понятия. Определение квадратного уравнения, формулы решения квадратных уравнений.
Самостоятельная деятельность учащихся. Решение задач по теме «Квадратные уравнения».
Использование новых информационных технологий. В качестве дополнительного иллюстративного материала показ на компьютере модели курса «Квадратные уравнения» (используется компьютерная модель 3.8. Решение уравнений графическим методом).
План урока
Этапы урока
Время, мин
Приёмы и методы
I. Этап актуализации знаний. Мотивация учебной проблемы
2
Беседа учителя
II. Основное содержание урока. Отработка с учащимися решения квадратных уравнений.
5
Объяснение учителя. Эвристическая беседа
III. Формирование умений и навыков. Отработка изученного материала
30
Решение задач. Ответы на вопросы учащихся
IV. Первичная проверка усвоения знаний. Рефлексия
5
Сообщение учителя. Сообщения учащихся
V. Домашнее задание
3
Запись на доске
Основное содержание урока
Первым и одним из основных методов решения уравнений является функционально-графический метод. Мы считаем, что для наглядности обучения удобно использовать модель 3.8.
В качестве параметров можно вводить следующие уравнения:
x2 – 6x + 8 = 0;
x2 – 4x + 3 = 0;
x2 – 2x – 3 = 0.
Очень полезно показать на модели 3.8 решение уравнения x2 – 2x – 3 = 0 разными способами.
Построить график функции y = x2 – 2x – 3 и найти точки пересечения его с осью Ох.
Решить графически уравнение x2 = 2x + 3.
Решить графически уравнение x2 – 3 = 2x.
Решить графически уравнение (x – 1)2 = 4 (то есть показать метод выделения полного квадрата).
Приведём систему упражнений, которая охватывает основные сюжеты, связанные с квадратными уравнениями. Эти упражнения составлены по линии нарастания трудности. После разбора этих сюжетов учащиеся будут готовы к написанию контрольной работы по теме «Квадратные уравнения».
Решите неполное квадратное уравнение:
x2 + 5x = 0;
–x2 + 8x = 0;
x2 – 9 = 0;
–2x2 + 11 = 0;
3x2 + 7 = 0;
6x2 = 0;
(x – 2)(x + 4) = 0;
x2 + 12x + 36 = 0;
4x2 – 3x + 7 = 2x2 + x + 7.
Составьте квадратное уравнение, которое является: А. полным и приведённым; Б. полным и неприведённым; В. неполным и приведённым; Г. неполным и неприведённым.
Докажите, что число 3 является корнем квадратного уравнения x2 – 4x + 3 = 0.
Докажите, что число –7 не является корнем уравнения 2x2 + x – 3 = 0.
При каких значениях параметра p уравнение (2p – 3)x2 + (3p – 6)x + p2 – 9 = 0 является: А. приведённым квадратным уравнением; Б. неполным неприведённым квадратным уравнением; В. неполным приведённым квадратным уравнением; Г. линейным уравнением?
При каких значениях параметра p уравнение x2 – 8x + p = 0 имеет корень, равный 4?
Решите уравнение
x2 – 5x + 6 = 0;
x2 + 2x – 7 = 0;
2x2 – 4x – 1 = 0;
(x – 2)2 = 3x – 8;
(3x – 1)(x + 3) + 1 = x(1 + 6x).
Решите уравнение с параметром p:
* x2 – (2p – 2)x + p2 – 2p = 0;
* x2 –
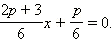
* x2 – 2px + p2 – 1 = 0.
* (p – 4)x2 + (2p – 4)x + p = 0.
* Докажите, что не существует такого значения параметра p, при котором уравнение x2 – px + p – 2 = 0 имело бы только один корень.
Ответы на вопросы
Какие уравнения называются неполными квадратными уравнениями?
Дайте определение квадратного уравнения.
Чему равен дискриминант квадратного уравнения?
Сколько корней имеет уравнение, если его дискриминант является положительным числом?
Сколько корней имеет уравнение, если его дискриминант равен нулю?
Сколько корней имеет уравнение, если его дискриминант является отрицательным числом?
Запишите формулы для вычисления корней квадратного уравнения.
Домашнее задание
Выучить формулы решения квадратных уравнений.
№ 988–999, № 1019–1021 из задачника А. Г. Мордковича, Т. Н. Мишустиной, Е. Е. Тульчинской, алгебра, 8 класс.
