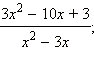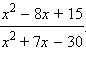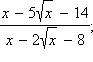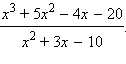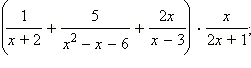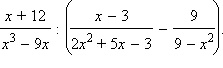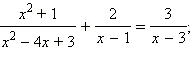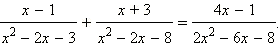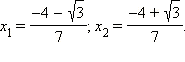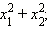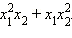Глава M. Методика
M.3.
M.3.4.
Тип урока: урок решения задачТема. Квадратный трёхчлен.
Цель урока. Научиться использовать на практике формулы сокращённого умножения при решении задач.
Основные понятия. Разложение квадратного трёхчлена на множители.
Самостоятельная деятельность учащихся. Применение теоремы о разложении квадратного трёхчлена на множители при решении задач.
Использование новых информационных технологий. В качестве дополнительного иллюстративного материала показ формул сокращённого умножения на компьютере (используется компьютерная модель 3.8. Решение уравнений графическим методом).
План урока
| Этапы урока |
Время, мин |
Приемы и методы |
| I. Этап актуализации знаний. Мотивация учебной проблемы |
2 |
Беседа учителя |
| II. Основное содержание урока. Формирование у учащихся представления о формулах сокращённого умножения |
10 |
Объяснение учителя. Эвристическая беседа |
| III. Формирование умений и навыков. Отработка изученного материала |
25 |
Решение задач.
Ответы на вопросы учащихся |
| IV. Первичная проверка усвоения знаний. Рефлексия |
5 |
Сообщение учителя.
Сообщение учащихся |
| V. Домашнее задание |
3 |
Запись на доске |
Методический комментарий учителю
Эта тема является основополагающей в разделе «Тождественные преобразования алгебраических выражений». Поэтому важно, чтобы учащиеся автоматически умели не только видеть в примерах формулы сокращённого умножения, но и применять их в других заданиях: в таких как решение уравнений, преобразование выражений, доказательство тождеств.
Приведём такую подборку упражнений, с помощью которых, на наш взгляд, удобно отработать на практике формулы сокращённого умножения. Обращаем ваше внимание, что упражнения идут по линии нарастания трудности материала (от простого к сложному). Эта подборка задач поможет правильно оценить и сильных, и слабых учеников.
В этой теме основное внимание уделяется разложению квадратного трёхчлена на множители. Достаточно много времени уделяется теореме: ax2 + bx + c = a(x – x1)(x – x2), где x1 и x2 – корни квадратного уравнения ax2 + bx + c = 0.
Поэтому, на наш взгляд, необходимо поработать с моделью 3.8, наглядно просмотреть графическое решение квадратных уравнений на следующих примерах:
- Решить уравнение x2 – 6x + 8 = 0;
- Решить уравнение x2 – 3x + 2 = 0;
- Решить уравнение x2 + 2x – 3 = 0.
При работе с моделью 3.8, разложение квадратного трёхчлена на множители пройдёт более понятно, так как корни соответствующего квадратного уравнения удобно наблюдать на картинке.
Кроме того, важное место занимает теорема Виета. Обычные школьные учебники содержат достаточно стандартную систему упражнений. Например, часто встречаются сюжеты типа:
- не используя формулу корней, найдите корни квадратного уравнения;
- составьте квадратное уравнение, корнями которого являются данные числа;
- назовите сумму и произведение корней уравнения;
- разложите на множители квадратный трёхчлен.
Конечно, эти задания являются обязательным минимумом, и мы их тоже обязательно включим в наш урок решения задач. Однако, на наш взгляд, необходимо разнообразить систему упражнений, включив в неё:
- нестандартные сюжеты, задачи с параметром;
- умение сокращать алгебраические дроби, используя формулу разложения квадратного трёхчлена на множители;
- умение упрощать алгебраические выражения.
Эти сюжеты выходят за рамки так называемых обязательных результатов обучения. Но именно они позволят расширить поле зрения учащегося, научить его мыслить в нестандартной ситуации, используя при этом изучаемый материал. Такие задания отмечены звездочкой.
Основное содержание урока
- Разложите на множители квадратный трёхчлен:
а) x2 – 12x + 24;
б) –x2 + 16x – 15;
в) 3x2 + 5x – 2;
г) –5x2 + 6x – 1.
- Сократите дробь:
а) 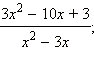
б) 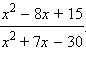
в) 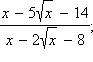
г) 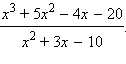
- Упростите выражение:
а) 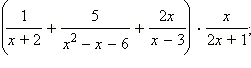
б) 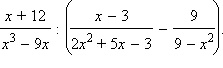
- Решите уравнение
а) 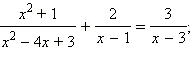
б) 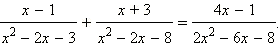
- Не используя формулу корней, найдите корни квадратного уравнения:
а) x2 + 3x + 2 = 0;
б) x2 – 9x + 20 = 0.
- Составьте квадратное уравнение, корнями которого являются числа:
а) x1 = 4; x2 = 2;
б) x1 = 3; x2 = –3 ;
в) 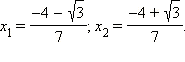
- * При каком значении параметра p сумма корней квадратного уравнения x2 + (p2 + 4p – 5)x – p = 0 равна нулю?
- * При каком значении параметра p произведение корней квадратного уравнения x2 + 3x + (p2 – 7p + 12) = 0 равно нулю?
- * Докажите, что уравнение ax2 + bx + c = 0 имеет корень, равный –1, если a – b + c = 0.
- * Пусть x1 и x2 – корни уравнения x2 – 9x – 17 = 0. Не решая уравнения, вычислите:
а) 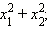
б) 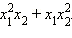
- * Дано уравнение x2 – (2p2 – p – 6)x + (8p – 1) = 0. Известно, что сумма его корней равна –5. Найдите значение параметра p.
- * Дано уравнение x2 – (p + 1)x + (2p2 – 9p – 12) = 0. Известно, что произведение его корней равно –21. Найдите значение параметра p.
- * При некотором значении параметра p корни квадратного уравнения 2px2 + (p2 – 9)x – 5p + 2 = 0 являются противоположными числами. Найдите эти корни.
- * При некотором значении параметра p корни квадратного уравнения 2px2 + 5x + p + 1 = 0 являются взаимно обратными числами. Найдите эти корни.
- * Один из корней квадратного уравнения 2x2 – 14x + p = 0 больше другого в 2,5 раза. Найдите значение параметра p и корни уравнения.
Ответы на вопросы
- Какую теорему мы сегодня изучили на уроке?
- При решении каких задач нам нужно уметь раскладывать квадратный трёхчлен на множители?
Домашнее задание
- Выучить теорему о разложении квадратного трёхчлена на множители.
- № 1157–1159, № 1160, № 1162, № 1164 из задачника 8 класса А. Г. Мордковича, Т. Н. Мишустиной, Е. Е. Тульчинской.


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".