 |
 |
Допустим теперь, что нас не интересует порядок, в котором идут выбранные элементы. Например, нужно из десяти человек выбрать троих дежурных. Такая операция называется неупорядоченной выборкой, или сочетанием, в отличие от упорядоченной выборки – размещений.
 |
 |
|
 |
 |
|
Символ 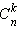 читается «це из эн по ка».
читается «це из эн по ка».
Формулу для 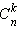 можно получить из следующих соображений.
можно получить из следующих соображений.
Из любого набора, содержащего
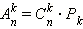 |
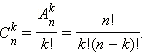 |

 |
|
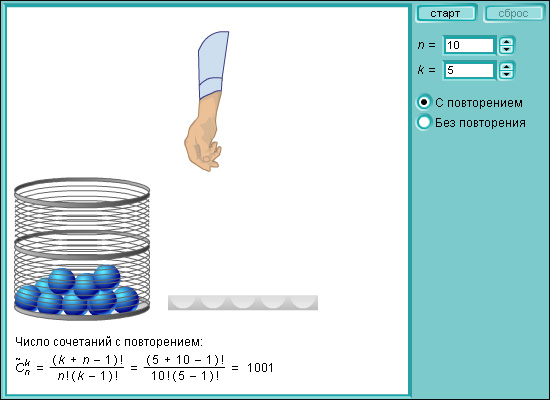
Модель 4.4.
Сочетания
|
Для проведения письменного экзамена нужно составить 3 варианта по 5 задач в каждом. Сколькими способами можно разбить 15 задач на 3 варианта?
Сколькими способами можно разместить 10 различных шаров по 4 ящикам так, чтобы в первом ящике оказалось 2 шара, во втором – 3, в третьем – 3 и в четвёртом снова два?
Для числа сочетаний 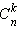 справедливы некоторые тождества, в частности:
справедливы некоторые тождества, в частности:
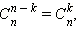
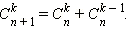
Запишем в «нулевой» строке число 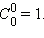 В первой строке напишем значения чисел
В первой строке напишем значения чисел 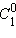 и
и 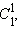 каждое из которых тоже равно 1, так, чтобы значение
каждое из которых тоже равно 1, так, чтобы значение 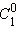 оказалось над промежутком между этими двумя числами. Во второй строке запишем числа
оказалось над промежутком между этими двумя числами. Во второй строке запишем числа 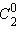 и
и 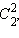 тоже равные 1, а между ними – число
тоже равные 1, а между ними – число 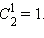 Обратим внимание, что число
Обратим внимание, что число 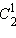 равно сумме двух чисел, стоящих над ним:
равно сумме двух чисел, стоящих над ним: 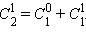 Продолжим построение, записывая в
Продолжим построение, записывая в 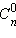 до
до 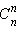 включительно.
включительно.
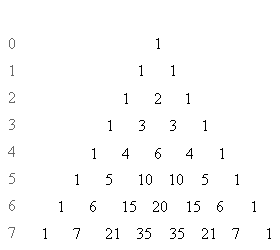 |
| Рисунок 4.2.3.1. Треугольник Паскаля
|
Полученный числовой треугольник называется треугольником Паскаля. Согласно свойству 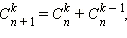 любое число в этом треугольнике равно сумме двух чисел, расположенных над ним в предыдущей строке.
любое число в этом треугольнике равно сумме двух чисел, расположенных над ним в предыдущей строке.
При помощи треугольника Паскаля удобно доказывать различные комбинаторные тождества.
На языке множеств утверждение, доказанное в задаче, выглядит по-другому.
Число подмножеств множества из |
Еще один интересный факт, связанный с треугольником Паскаля, мы приведём здесь без доказательства:
Бином Ньютона
|
Приведённое тождество называется биномом Ньютона.
Как и в случае с размещениями, существует понятие числа сочетаний с повторениями. Рассмотрим его на следующем примере.
В палитре художника 8 различных красок. Художник берет кистью наугад любую из красок и ставит цветное пятно на ватмане. Затем берет следующую кисть, окунает её в любую из красок и делает второе пятно по соседству. Сколько различных комбинаций существует для шести пятен? Порядок пятен на ватмане не важен.
 |
Вообще, можно сформулировать следующее правило.
 |
 |
|
 |
 |
|
 |
 |
 |

