 |
 |
Основные способы решений неравенств с модулем во многом совпадают с методами решения аналогичных уравнений. Единственное отличие, пожалуй, связано с тем, что, решая неравенства с модулем (как, впрочем, и неравенства вообще), нужно очень внимательно совершать равносильные переходы и следить не только за тем, чтобы не приобрести новые решения, но и за тем, чтобы не потерять уже имеющиеся.
Стандартный путь решения неравенств с модулем заключается в том, что координатная прямая разбивается на промежутки (границами этих промежутков являются нули подмодульных выражений), а затем неравенство решается на каждом из промежутков.
Этот метод работает всегда. Правда, в отдельных случаях может быть затруднена его техническая реализация, например, очень тяжело или невозможно найти корни подмодульных выражений и пр. Однако, это сложности иного плана. Нужно понимать, что раскрытие модуля по определению неизменно приводит к цели. Конечно же, этот метод не является оптимальным: в условиях конкурсного экзамена важен не только результат, но и то время, которое потрачено на его получение.
Рассмотрим методы, не связанные с поиском нулей функций, стоящих под знаком модуля.
Рассмотрим неравенство 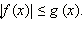 Очевидно, что те
Очевидно, что те 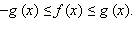 Таким образом, имеем
Таким образом, имеем
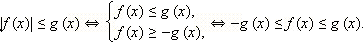 |
Аналогично можно рассмотреть неравенство 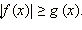 Неравенство выполнено для тех
Неравенство выполнено для тех 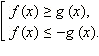
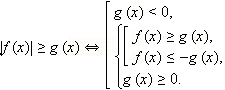 |
Заметим, что последняя совокупность является равносильной нашему неравенству и при
Как видно, в простых случаях особых преимуществ метод перехода к равносильной системе не имеет, но иногда его преимущества весьма заметны.
 |
 |
 |

