 |
 |
Пожалуй, самым важным методом решения уравнений любого типа является введение нового неизвестного, относительно которого уравнение имеет более простой вид, легко приводящийся к элементарному типу.
Перечислим наиболее часто встречающиеся типы замен.
Замена
В частности, с помощью замены
Замена 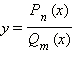 (дробно-рациональная замена). Здесь, как и всегда,
(дробно-рациональная замена). Здесь, как и всегда, 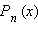 и
и 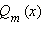 − многочлены степеней
− многочлены степеней
В частности, с помощью широко распространённой замены 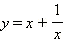 решаются так называемые возвратные уравнения, то есть уравнения вида
решаются так называемые возвратные уравнения, то есть уравнения вида
Покажем, как это делается. Так как
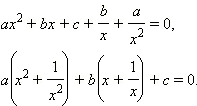 |
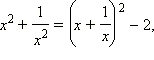 то после замены
то после замены 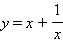 уравнение сводится к квадратному
уравнение сводится к квадратному 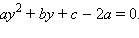
Дадим два практических совета.
Совет 1. Замену переменных нужно делать сразу, при первой же возможности.
Совет 2. Уравнение относительно новой переменной нужно решать до конца, и лишь затем возвращаться к старому неизвестному.
 |
 |
 |

