Учебник. Свойства определенного интеграла

Доопределим понятие интеграла при a ≥ b следующими равенствами: $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\mathrm{-}\underset{b}{\overset{a}{\int }}f\left(x\right)dx\mathrm{,}$ $\underset{a}{\overset{a}{\int }}f\left(x\right)dx=0\mathrm{.}$

Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.

• Если функция интегрируема на [a; b], то она интегрируема на любом отрезке $\left[x_1\mathrm{; }{x}_2\right]\subset \left[a\mathrm{; }b\right]\mathrm{.}$
• Для любых a, b и c $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a}{\overset{c}{\int }}f\left(x\right)dx+\underset{c}{\overset{b}{\int }}f\left(x\right)dx\mathrm{.}$
• Интеграл обладает свойством линейности: для любых функций f (x) и g (x) и любой постоянной A $\underset{a}{\overset{b}{\int }}\left(f\left(x\right)+g\left(x\right)\right)dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx+\underset{a}{\overset{b}{\int }}g\left(x\right)dx\mathrm{,}$ $\underset{a}{\overset{b}{\int }}Af\left(x\right)dx=A\underset{a}{\overset{b}{\int }}f\left(x\right)dx\mathrm{.}$
• Если f (x) и g (x) интегрируемы на [a; b], то f (x) ċ g (x) также интегрируема на этом отрезке.
• Если f (x) – периодическая функция с периодом T, то для любого a $\underset{a}{\overset{a+T}{\int }}f\left(x\right)dx=\underset{0}{\overset{T}{\int }}f\left(x\right)dx\mathrm{.}$

Свойства определенного интеграла

Для определенных интегралов верны также следующие оценки (предполагается, что функции f и g интегрируемы на [a; b]).

• Если f (x) ≥ g (x), то $\underset{a}{\overset{b}{\int }}f\left(x\right)dx\ge \underset{a}{\overset{b}{\int }}g\left(x\right)dx\mathrm{.}$ В частности, если f (x) ≥ 0, то $\underset{a}{\overset{b}{\int }}f\left(x\right)dx\ge 0\mathrm{.}$
• Если f (x) ≥ 0 для любого $x\in \left[a\mathrm{; }b\right]\mathrm{}$  и существует $x_0\in \left[a\mathrm{; }b\right]$ такое, что $f\left(x_0\right)>0\mathrm{,}$  причем f (x) непрерывна в $x_0\mathrm{,}$  то $\underset{a}{\overset{b}{\int }}f\left(x\right)dx>0\mathrm{.}$
• |f (x)| интегрируема на [a; b], причем $\left|\underset{a}{\overset{b}{\int }}f\left(x\right)dx\right|\le \underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx\mathrm{.}$
• Если на отрезке [a; b] m ≤ f (x) ≤ M, то $m\left(b-a\right)\le \underset{a}{\overset{b}{\int }}f\left(x\right)dx\le M\left(b-a\right)\mathrm{.}$

Численное вычисление определенного интеграла при помощи формулы трапеций

Для вычисления определенных интегралов на компьютере нередко используют приближенную формулу трапеций: $\underset{a}{\overset{b}{\int }}f\left(x\right)dx\approx \frac{b-a}{n}\left(\frac{f\left(a\right)}{2}+f\left(x_1\right)+\mathrm{...}+f\left(x_n\right)+\frac{f\left(b\right)}{2}\right)\mathrm{.}$

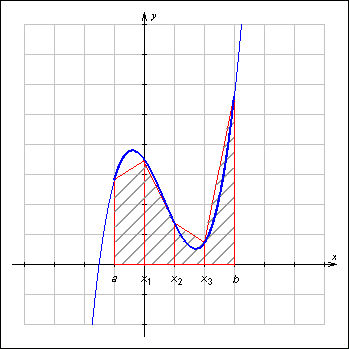
Ее смысл состоит в том, что криволинейные трапеции заменяются обычными, площадь каждой из которых равна $\frac{f\left(x_i\right)+f\left(x_{i-1}\right)}{2}\left(x_i-x_{i-1}\right)\mathrm{.}$