Учебник. Выпуклость функции и точки перегиба

Непрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x₁ и x₂ из этого отрезка $f\left(\frac{x_1+x_2}{2}\right)\ge \frac{f\left(x_1\right)+f\left(x_2\right)}{2}\mathrm{.}$

Выпуклая вверх функция

Другими словами, если для любых точек x₁ и x₂ отрезка [a; b] секущая AB проходит под графиком функции f (x), то функция f выпукла вверх.

Аналогично определяется функция, выпуклая вниз.

Дважды дифференцируемая на [a; b] функция f (x) выпукла вверх, если для любого $x\in \left[a\mathrm{; }b\right]$ $f^{\mathrm{\prime \prime }}\left(x\right)\le 0\mathrm{.}$

Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого $x\in \left[a\mathrm{; }b\right]$ $f^{\mathrm{\prime \prime }}\left(x\right)\ge 0\mathrm{.}$

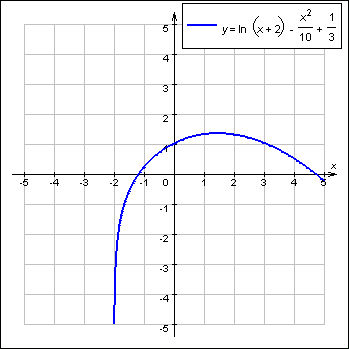
Так, вторая производная функции $y$ равна $f^{\mathrm{\prime \prime }}\left(x\right)=2>0\mathrm{,}$ откуда следует, что квадратичная функция выпукла вниз на всей области определения.

Пусть функция f (x) непрерывна в точке $x_0$ и имеет в этой точке конечную или бесконечную производную. Тогда точка $x_0$ называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.

Необходимое условие наличия точки перегиба. Если $x_0$ – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то $f^{\mathrm{\prime \prime }}\left(x_0\right)=0\mathrm{.}$

Достаточные условия наличия точки перегиба.

Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке $x_0\mathrm{.}$  Если $f^{\mathrm{\prime \prime }}\left(x_0\right)$ меняет знак при переходе через точку $x_0\mathrm{,}$  то $x_0$ – точка перегиба функции f (x).

Если $f^{\mathrm{\prime \prime }}\left(x_0\right)=0\mathrm{,}$   $f^{\left(3\right)}\left(x_0\right)\ne 0\mathrm{,}$ то $x_0$ – точка перегиба функции f (x).

 

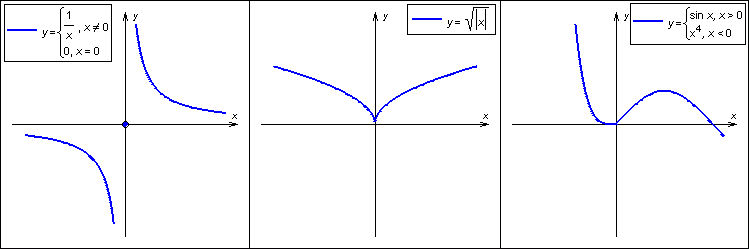
В заключение приведём примеры, когда точка x₀ не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:

• если функция разрывна в точке $x_0$ (например $f=\{\begin{array}{c}\frac{1}{x}\mathrm{ при }x\ne 0\\ 0\mathrm{,}x=0\end{array}\mathrm{,}$    $x_0=0$ );
• в случае угловой точки (например, $f=\{\begin{array}{c}sinx\mathrm{,}x\ge 0\\ x^4\mathrm{,}x<0\end{array}$    $x_0=0\mathrm{).}$

Не являются точками перегиба и точки возврата, например точка $x_0=0$ у функции $y=\sqrt{\mathrm{|}x\mathrm{|}}$

 

Все вышеперечисленные случаи изображены на рисунке.

Точки, не являющиеся точками перегиба: точка разрыва, точка возврата, угловая точка