
Учебник. Гиперболические функции
Функция
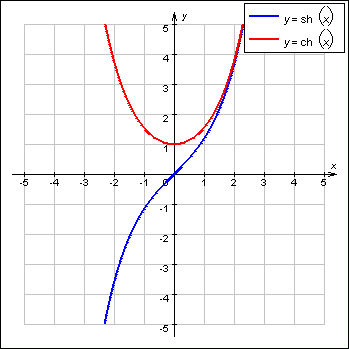
Подобно тому, как тригонометрические синус и косинус являются координатами точки на координатной окружности, гиперболические синус и косинус являются координатами точки на гиперболе.
Эти функции определены и непрерывны на всей числовой оси. Гиперболический синус является нечетной функцией, возрастающей на всей числовой оси. Гиперболический косинус является четной функцией, убывающей на
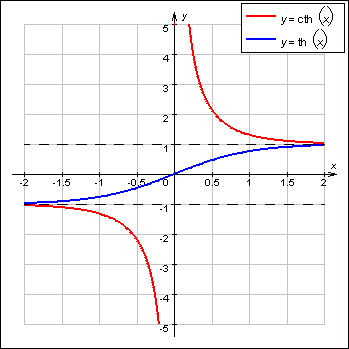
По аналогии с тригонометрическими функциями определены гиперболические тангенс и котангенс:
Тангенс определён на всей числовой оси, котангенс – при всех x ≠ 0
Приведём некоторые формулы, связанные с гиперболическими функциями.
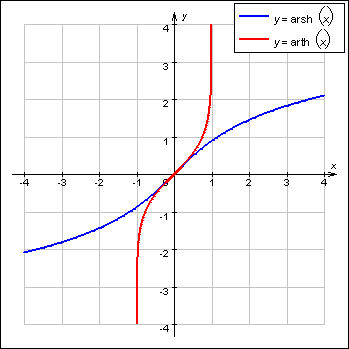
Функции, обратные гиперболическим синусу и тангенсу, определены и непрерывны на всей числовой оси. Они обозначаются соответственно arsh x и arth x. У гиперболического косинуса определены сразу две обратные функции: arch– x при x ≤ 0 и arch+ x при x ≥ 0.
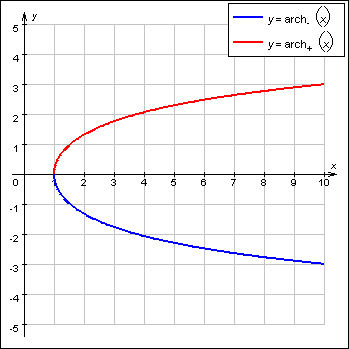
В заключение приведём формулы для обратных гиперболических функций:
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".