Учебник. Координатная окружность

Тригонометрическими называются функции вида y = sin x, y = cos x, y = tg x, y = ctg x и их комбинации.

 

Координатная окружность

Одной и той же точке можно сопоставить длину дуги, пробегаемой как в положительном, так и в отрицательном направлении

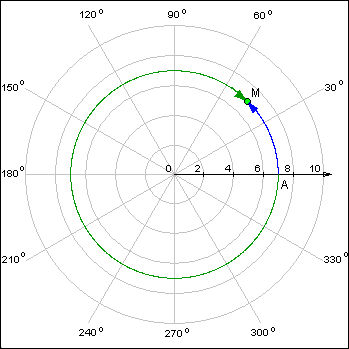
Назовем координатной окружность единичного радиуса, на который выбраны начало отсчета A и направление отсчета (обычно в качестве положительного выбирают направление обхода против часовой стрелки). Произвольному числу $x\in \left[0\mathrm{; }2\pi \right)$ ставится в соответствие точка на окружности M (x) такая, что длина дуги, соединяющей начало отсчета A с этой точкой, равняется x. Если же число x принадлежит промежутку $\left[2\pi n\mathrm{; }2\pi \left(n+1\right)\right)\mathrm{,}$   $n\in \mathbb{Z}\mathrm{,}$   то ему в соответствие ставится точка M (x), длина дуги до которой равняется x – 2πn. Таким образом, всем числам x + 2πn, $n\in \mathbb{Z}\mathrm{,}$ геометрически ставится в соответствие одна и та же точка M (x) координатной окружности.

Симметрия точек на координатной окружности

Точки B (x) и C (–x) симметричны относительно оси OA, где O – центр окружности. Точки B (x) и D (π + x) симметричны относительно центра окружности O.

Центральный угол α (выраженный в радианах) определяется как $\alpha =\frac{l}{R}\mathrm{.}$ Таким образом, длина дуги, содержащей центральный угол α, равна l = αR.

Отношение длины окружности C к ее диаметру постоянно и равно $\pi =\frac{C}{2R}$ Число π – трансцендентное, π = 3,14159... Используя число π, можно записать выражение для длины окружности: $C=2\pi R$

Площадь сектора равна $S=\frac{1}{2}\alpha R^2$ а площадь всего круга (α = 2π) равна S = πR².