Открытая Математика. Функции и Графики. Квадратное уравнение

Квадратное уравнение

Уравнение ax² + bx + c = 0, где a ≠ 0, называется квадратным уравнением.

Выделив полный квадрат, получим уравнение $a x^{2} + b x + c = a {(x + \frac{b}{2 a})}^{2} - \frac{D}{4 a} = 0 .$ Если $D \geq 0,$ то отсюда следует, что $x + \frac{b}{2 a} = ± \sqrt{\frac{D}{4 a^{2}}} = ± \frac{\sqrt{D}}{2 a}$ или $x = \frac{- b \pm \sqrt{D}}{2 a} .$

Мы получили формулу корней квадратного уравнения (формулу Виета).

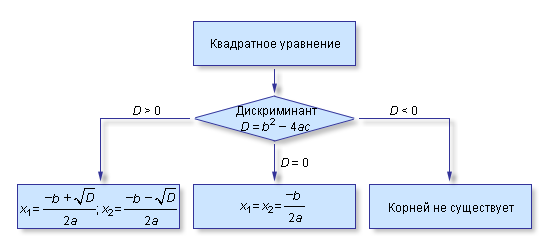
Алгоритм поиска корней квадратного уравнения

При D > 0 существуют два корня x₁ и x₂. При D = 0 корни квадратного уравнения совпадают: x₁ = x₂. Наконец, при D < 0 равенство ${(x + \frac{b}{2 a})}^{2} = \frac{D}{4 a^{2}}$ невозможно, и корней у квадратного уравнения не существует.

Если D ≥ 0, то квадратичную функцию можно разложить на множители: $y = a {(x + \frac{b}{2 a})}^{2} - \frac{D}{4 a} = a (x + \frac{b}{2 a} + \frac{\sqrt{D}}{2 a}) (x + \frac{b}{2 a} - \frac{\sqrt{D}}{2 a}) .$ Таким образом y = a (x – x₁) (x – x₂), где $x_{1} = - \frac{b}{2 a} - \frac{\sqrt{D}}{2 a},$ $x_{2} = - \frac{b}{2 a} + \frac{\sqrt{D}}{2 a} .$ Если D = 0, то $y = a {(x - x_{0})}^{2} .$ Если D < 0, то квадратный трехчлен нельзя разложить на множители.

Движение по параболе

Теорема Виета. Для того чтобы числа x₁ и x₂ были корнями уравнения ax² + bx + c = 0 (a ≠ 0), необходимо и достаточно, чтобы выполнялись равенства: ${\begin{matrix} x_{1} + x_{2} = - \frac{b}{a}, \\ x_{1} ċ x_{2} = \frac{c}{a} . \end{matrix}$

Необходимость. Пусть числа $x_{1}$ и $x_{2}$ являются корнями уравнения $a x^{2} + b x + c = 0$ (a ≠ 0). Тогда $x_{1} = - \frac{b}{2 a} - \frac{\sqrt{D}}{2 a},$ $x_{2} = - \frac{b}{2 a} + \frac{\sqrt{D}}{2 a} .$ Имеем $x_{1} + x_{2} = - \frac{b}{a},$ $x_{1} ċ x_{2} = \frac{b^{2} - D}{4 a^{2}} = \frac{c}{a} .$
Достаточность. Пусть имеется система ${\begin{array}{l} x_{1} + x_{2} = - \frac{b}{a}, \\ x_{1} x_{2} = \frac{c}{a} . \end{array}$ Из первого равенства $x_{2} = - \frac{b}{a} - x_{1} .$ Подставляя это значение во второе равенство, получим $x_{1} (- \frac{b}{a} - x_{1}) = \frac{c}{a},$ откуда $a x_{1}^{2} + b x_{1} + c = 0 .$ Значит, число $x_{1}$ является корнем квадратного уравнения $a x^{2} + b x + c = 0 .$ Аналогично доказывается, что $x_{2}$ – также корень этого уравнения.

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Квадратное уравнение

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ