Учебник. Периодические функции

Функция f (x) называется периодической с периодом T ≠ 0, если выполняются два условия:

• если $x\in D$ , то x + T и x – T также принадлежат области определения D (f (x));
• для любого $x\in D$ выполнено равенство f (x + T) = f (x).

Поскольку $x-T\in D\mathrm{,}$ то из приведенного определения следует, что f (x – T) = f (x).

Если T – период функции f (x), то очевидно, что каждое число nT, где $n\in \mathbb{Z}$ , n ≠ 0, также является периодом этой функции.

Наименьшим положительным периодом функции называется наименьшее из положительных чисел T, являющихся периодом данной функции.

График периодической функции обычно строят на промежутке [x₀; x₀ + T), а затем повторяют на всю область определения.

Хорошим примером периодических функций могут служить тригонометрические функции y = sin x, y = cos x (период этих функций равен 2π), y = tg x (период равен π) и другие. Функция y = const также является периодической. Для нее периодом является любое число T ≠ 0.

Не следует думать, что периодическими бывают только тригонометрические функции. Функция y = [x], где [x] – целая часть числа x (наибольшее целое число, не превосходящее x) позволяет определить функцию y = {x}, где {x} – дробная часть числа x. По определению {x} = x – [x] (например, {3,7} = 0,7, {–6} = 0, {–4,2} = –4,2 – (–5) = 0,8). Дробная часть числа – функция с периодом T = 1.

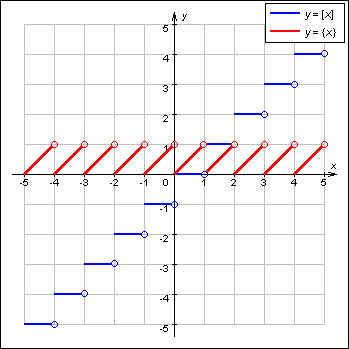
В заключение отметим свойства периодических функций.

• Если f (x) – периодическая функция с периодом T, то функция g (x) = A · f (kx + b), где k ≠ 0 также является периодической с периодом $T_1=\frac{T}{k}$ .
• Пусть функции f₁ (x) и f₂ (x) определены на всей числовой оси и являются периодическими с периодами T₁ > 0 и T₂ > 0. Тогда если $\frac{T_2}{T_1}\in \mathbb{Q}\mathrm{,}$  то функция $\mathrm{f }$ периодическая с периодом T, равным наименьшему общему кратному чисел $T_1$ и $T_2\mathrm{.}$