Открытая Математика. Алгебра. Непрерывные распределения вероятностей

Непрерывные распределения вероятностей

Если случайная величина A может принимать любые значения в интервале (a; b), то такая случайная величина называется непрерывной.

Вернемся к стрелку, на примере которого мы вводили понятие дискретного распределения вероятностей. Тогда мы рассматривали результат его стрельбы в виде номера круга, в который он попал. Теперь же представим, что, попадая в мишень, стрела оставляет на мишени точку. Вероятность того, что стрела два раза попадёт в одно и то же место, очень мала, поэтому можно считать, что точки не пересекаются. Мы увидим примерно такую картинку.

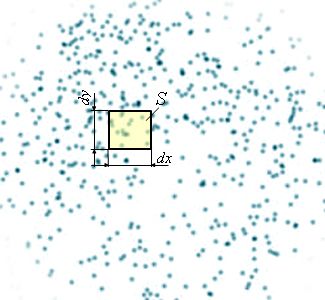
Если разделить количество точек, попавших в небольшой квадрат площадью ΔS = ΔxΔy, на общее количество выстрелов, то получится вероятность попадания в выделенный квадрат. Запишем: $p (Δ S) = \frac{Δ N}{N} .$

Здесь мы предполагаем, что площадка ΔS настолько мала, что попадания внутри этой площадки распределены равномерно. Тогда вероятность попадания в маленький квадрат будет зависеть от координаты центра этого квадрата и станет пропорциональной его площади: $p (Δ S) = φ (x, y) Δ S .$

При устремлении площади квадратика к нулю (вспомните школьный курс интегрального исчисления) конечные разности нужно заменить на дифференциалы: $lim_{Δ S \to 0} Δ S = d S = d x ċ d y .$ Итак, $p (d S) = φ (x, y) d x d y .$ Функция φ (x, y), которая входит в это равенство, называется плотностью вероятности. Домноженная на дифференциал площади, она равна вероятности попадания стрелка в бесконечно малую окрестность точки (x, y).

Если нам нужно будет узнать вероятность, с которой стрелок попадает в площадку мишени, на которой плотность вероятности нельзя считать постоянной, эту функцию придётся интегрировать.

Плотность вероятности существует и для распределений, зависящих от одной переменной. Рассмотрим это на следующем примере.

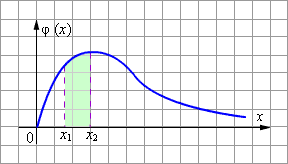
Пусть x – это расстояние от точки, в которую попал стрелок, до центра мишени. Тогда p (dx) = φ (x) dx – вероятность попадания стрелком в окрестность dx точки x. Вероятность того, что стрелок «попадёт» в промежуток [x₁; x₂], $p (x_{1} \leq x \leq x_{2}) = \int_{x_{1}}^{x_{2}} φ (x) d x .$

Отсюда следует важное свойство плотности вероятности. Поскольку попадание случайной величины x в интервал (–∞; +∞) – событие достоверное, то справедливо свойство нормировки плотности распределения вероятности.

$\int_{- ∞}^{+ ∞} φ (x) d x = 1 .$

Для некоторого случайного процесса график зависимости плотности вероятности от значения переменной x выглядит следующим образом:

Найти величину a.

Если φ (x) – плотность распределения вероятности, то $\int_{- ∞}^{+ ∞} φ (x) d x = 1 .$ В нашем случае $φ (x) = {\begin{array}{l} a, 0 \leq x \leq 2, \\ 0, x > 2, x < 0. \end{array}$ Следовательно, $\int_{- ∞}^{+ ∞} φ (x) d x = \int_{- ∞}^{0} 0 ċ d x + \int_{0}^{2} a ċ d x + \int_{2}^{+ ∞} 0 ċ d x = 2 a = 1.$ Отсюда $a = \frac{1}{2} .$

Обратите внимание, что интеграл от функции равен площади под графиком функции. Следовательно, площадь под графиком функции плотности вероятности φ (x) равна единице.

Ответ. $a = \frac{1}{2} .$

Математическое ожидание величины x для непрерывного распределения, задаваемого плотностью φ (x), определяется формулой $M_{x} = \int_{- ∞}^{+ ∞} x ċ φ (x) d x,$ а дисперсия – формулой $D_{x} = \int_{- ∞}^{+ ∞} {(x - M_{x})}^{2} φ (x) d x .$

Среднеквадратичное отклонение по-прежнему задается формулой $σ_{x} = \sqrt{D_{x}} .$

Вообще, в том случае, если плотность распределения случайной величины x равна φ (x), математическое ожидание какой-либо функции f (x) этой случайной величины задаётся формулой $M_{f (x)} = \int_{- ∞}^{+ ∞} f (x) φ (x) d x .$

Так же, как и для дискретных процессов, для непрерывной случайной величины существуют несколько характерных распределений вероятностей.

1. Постоянное распределение

Распределение, частный случай которого приведён в примере 1, называется постоянным распределением. Его плотность принимает одно и то же значение $φ (x) = \frac{1}{b - a}$ на некотором отрезке x ∈ [a; b] и равна нулю вне этого отрезка. Учитывая свойство нормировки плотности распределения $\int_{- ∞}^{+ ∞} φ (x) d x = 1,$ становится ясно, что значение φ (x) полностью задаётся шириной отрезка [a; b].

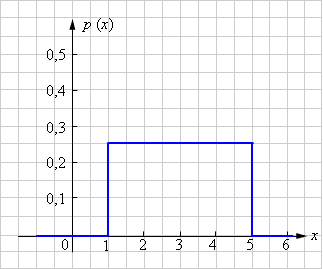
Плотность вероятности постоянного распределения при a = 1, b = 5

Вычислить математическое ожидание, дисперсию, среднеквадратичное отклонение случайной величины x, а также среднее значение величины $x^{2}$ для постоянного распределения $φ (x) = \frac{1}{b - a} .$

Математическое ожидание для непрерывного распределения можно вычислить по формуле $M_{x} = \int_{- ∞}^{+ ∞} x ċ φ (x) d x .$ В нашем случае $M_{x} = \int_{- ∞}^{+ ∞} x ċ φ (x) d x = \int_{a}^{b} \frac{x}{b - a} d x = {\frac{x^{2}}{2 (b - a)} |}_{a}^{b} = \frac{b^{2}}{2 (b - a)} - \frac{a^{2}}{2 (b - a)} = \frac{a + b}{2} .$ Этого и следовало ожидать: математическое ожидание величины x должно лежать в точности посередине отрезка [a; b].

Дисперсия $D_{x} = \int_{- ∞}^{+ ∞} {(x - M_{x})}^{2} φ (x) d x = \int_{a}^{b} {(x - \frac{a + b}{2})}^{2} \frac{1}{b - a} d x \underset{y = x - \frac{a + b}{2}}{=======} \frac{1}{b - a} \int_{\frac{a - b}{2}}^{\frac{b - a}{2}} y^{2} d y = {\frac{y^{3}}{3 (b - a)} |}_{\frac{a - b}{2}}^{\frac{b - a}{2}} = \frac{{(b - a)}^{2}}{12} .$ Среднеквадратичное отклонение $σ_{x} = \sqrt{D_{x}} = \frac{b - a}{2 \sqrt{3}} .$ Наконец, среднее значение величины $x^{2}$ равно $M_{x^{2}} = \int_{- ∞}^{+ ∞} x^{2} ċ φ (x) d x = \int_{a}^{b} \frac{x^{2}}{b - a} d x = {\frac{x^{3}}{3 (b - a)} |}_{a}^{b} = \frac{a^{2} + a b + b^{2}}{3} .$

Ответ. $\frac{a + b}{2};$ $\frac{{(b - a)}^{2}}{12};$ $\frac{b - a}{2 \sqrt{3}};$ $\frac{a^{2} + a b + b^{2}}{3} .$

2. Экспоненциальное, или показательное распределение

Рассмотрим прохождение потока частиц через какое-либо вещество. Часть частиц будет поглощаться веществом. Разделим мысленно среду на тонкие пластинки, и пусть, проходя через каждую пластинку, количество частиц в потоке уменьшается в p раз. Тогда, пройдя k пластинок, от начального потока останется лишь p^k-я часть.

В реальных условиях процесс поглощения частиц всегда случаен. Можно сказать, что вероятность обнаружить частицу после прохождения через k пластинок равна $p (k) = a p^{k},$ где a – некоторая константа, значение которой мы найдём позже. Введём новую величину λ = –ln p, тогда $p = e^{- λ}$ и $p (k) = a e^{- λ k} .$ Устремим ширину пластинки к нулю, одновременно увеличивая количество пластинок. В этом случае можно записать, что вероятность обнаружить частицу на глубине x внутри среды равна $p (x) = a e^{- λ x}$ (x > 0). Плотность распределения величины x можно вычислить при наложении дополнительного условия $\int_{- ∞}^{+ ∞} φ (x) d x = 1.$ Так как выражение $\int_{0}^{+ ∞} a e^{- λ x} d x = {- \frac{a}{λ} e^{- λ x} |}_{0}^{+ ∞} = - \frac{a}{λ} (0 - 1) = \frac{a}{λ}$ равно единице по условию нормировки, то a = λ.

Плотность вероятности экспоненциального распределения описывается формулой $p (x) = λ e^{- λ x} .$

Его математическое ожидание и среднеквадратичное отклонение можно получить путём интегрирования по частям. Пропуская вычисления, запишем сразу результат: $M_{x} = \frac{1}{λ}, σ = \frac{1}{λ} .$

Плотность вероятности экспоненциального распределения

Вероятность того, что лампочка перегорит ровно через t дней, подчиняется закону p₀ (t) = 0,02 e^–0,02t. Найти вероятность того, что 100 дней лампочка будет работать безотказно.

Найдём сначала вероятность перегорания за 100 дней:

p (100) = \int_{0}^{100} 0,02 e^{- 0,02 t} d t = 1 - e^{- 0,02 ċ 100} = 1 - e^{- 2} = 1 - 0,135 .

Тогда вероятность безотказной работы

p (\bar{100}) = 0,135.

Ответ. 0,135

3. Рассматривая в предыдущем параграфе дискретные распределения, мы говорили о том, что если распределение вероятностей вызвано сложением большого количества случайных событий, каждое из которых мало влияет на результат, то это, скорее всего, распределение Пуассона. В аналогичном непрерывном случае получается распределение Гаусса, которое часто называют нормальным распределением.

Плотность вероятности нормального распределения имеет вид:

φ (x) = \frac{1}{\sqrt{2 π} σ} e^{- \frac{{(x - a)}^{2}}{2 σ^{2}}} .

В этой формуле a – математическое ожидание величины x, а σ – ее среднеквадратичное отклонение. Вывод этой формулы из распределения Пуассона основан на формуле Стирлинга и разложении в ряд Тейлора; для школьного курса он слишком сложен, и поэтому мы его опускаем.

Плотность вероятности нормального распределения

Сумма двух нормальных распределений с параметрами $a_{1}, σ_{1}$ и $a_{2}, σ_{2}$ также является нормальным распределением с параметрами $a = a_{1} + a_{2}$ и $σ^{2} = σ_{1}^{2} + σ_{2}^{2} .$

Показания счётчика Гейгера, регистрирующего количество пролетевших сквозь него за 1 секунду элементарных частиц, подчиняются распределению $φ (N) \approx 0,00127 e^{- \frac{{(N - 1000)}^{2}}{5000}} .$ Найдите математическое ожидание показаний счётчика.

Предположим, что распределение $φ (N) \approx 0,00798 e^{- \frac{{(N - 1000)}^{2}}{5000}}$ является нормальным. В этом случае a = 1000, σ = 50. Проверкой убеждаемся, что коэффициент перед экспонентой равен $\frac{1}{\sqrt{2 π} σ},$ то есть распределение действительно является нормальным. Тогда $M_{N} = 1000$ частиц в секунду.

Ответ. 1000.

Определите среднее значение скорости молекул газа, если закон распределения скоростей молекул задаётся формулой Максвелла $φ (υ) = 4 \sqrt{\frac{k^{3}}{π}} υ^{2} e^{- k υ^{2}} .$

Среднее значение скорости равно $\bar{υ} = \int_{0}^{+ \infty} υ φ (υ) d υ = \frac{2}{\sqrt{k π}} .$

Для данного выше распределения Максвелла вычислить дисперсию.

Имеем: $\bar{{(υ - \bar{υ})}^{2}} = \int_{0}^{+ \infty} {(υ - \bar{υ})}^{2} φ (υ) d υ = \int_{0}^{+ \infty} υ^{2} φ (υ) d υ - {(\bar{υ})}^{2} = \frac{3}{2 k} - \frac{4}{π k} .$

Ответ. $\frac{3}{2 k} - \frac{4}{π k} .$

Нормальному распределению подчиняются случайные ошибки измерений.

4. Частным случаем нормального распределения является логарифмически нормальное. Оно легко получается из нормального заменой x на ln x:

φ (ln x) d (ln x) = \frac{1}{\sqrt{2 π} σ} e^{- \frac{{(ln x - a)}^{2}}{2 σ^{2}}} d (ln x) = \frac{1}{\sqrt{2 π} σ x} e^{- \frac{{(ln x - a)}^{2}}{2 σ^{2}}} d x .

Здесь учтено, что $\frac{d (ln x)}{d x} \equiv {(ln x)}^{′} = \frac{1}{x} .$

Плотность логарифмически нормального распределения $φ (x) = \frac{1}{\sqrt{2 π} σ x} e^{- \frac{{(ln x - a)}^{2}}{2 σ^{2}}} .$

Плотность вероятности логнормального распределения Распределения вероятностей

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Непрерывные распределения вероятностей

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ