Открытая Математика. Алгебра. Дискретные распределения вероятностей

Дискретные распределения вероятностей

Пусть случайная величина принимает дискретные значения. К таким величинам, например, относятся количество очков при бросании кубика или количество угаданных номеров в лотерее «Спортлото». Вспомним, что закон распределения случайной величины образуют множество всевозможных её значений и вероятности, с которыми эта случайная величина принимает свои значения. Законы распределения могут быть вычислены исходя из логики процесса или измерены, если у нас есть достаточно большая статистическая выборка. Но для некоторых часто встречающихся типов процессов можно не выводить распределение, а использовать стандартное похожее. Рассмотрим наиболее известные из них.

1. Геометрическое распределение

Будем бросать кубик до тех пор, пока не выпадет 1. Посчитаем, с какой вероятностью это случится ровно за N бросков.

Для первого броска (N = 1), очевидно, вероятность успеха p (1) = 1/6.

Для второго (N = 2) это вероятность успеха во втором броске и неудачи в первом: $p (2) = p (2 | \bar{1}) = (1 - \frac{1}{6}) \frac{1}{6} = \frac{5}{36} .$

Аналогично, для третьего броска $p (3) = p (3 | \bar{1} \bar{2}) = (1 - \frac{1}{6}) (1 - \frac{1}{6}) \frac{1}{6} = \frac{25}{216} .$

Вообще, для n-го броска $p (n) = {(1 - \frac{1}{6})}^{n - 1} ċ \frac{1}{6} = p {(1 - p)}^{n - 1},$ где p – вероятность успеха в единичном испытании.

Закон распределения $p (n) = p {(1 - p)}^{n - 1},$ где p – вероятность успеха в единичном испытании, называется геометрическим.

Математическое ожидание и дисперсия для этого распределения: $M_{x} = \frac{1}{p},$ $D_{x} = \frac{1 - p}{p^{2}} .$

В нашем примере $M_{x} = \frac{1}{p} = \frac{1}{1 / 6} = 6$ означает, что, в среднем, за шесть бросков 1 очко выпадет ровно 1 раз.

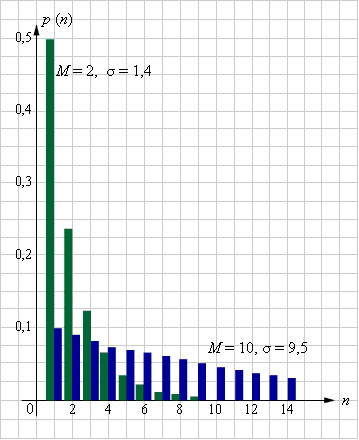
Геометрическое распределение при различных p и n

Ролик кодового замка содержит N возможных цифр, из которых нужно выбрать одну. С какой вероятностью его можно открыть точно с k-го раза?

Вероятность правильного единичного выбора $p = \frac{1}{N};$ распределение, очевидно, геометрическое, поэтому $p (k) = {(1 - \frac{1}{N})}^{k - 1} \frac{1}{N} .$

Если замок состоит из нескольких независимых роликов, то вероятность его случайного открывания подчиняется уже другому распределению – биномиальному.

2. Биномиальное распределение, часто возникающее в случайных процессах, можно получить так. Бросаем монету N раз и считаем вероятность того, что k раз из N выпала решка (будем обозначать это событие буквой P, а противоложное ему – выпадение герба – буквой О). Подумаем, какие распределения в этом случае можно считать равновероятными. Допустим, мы кинули монету три раза, при этом могли возникнуть такие комбинации:

    ООО;
    ООР; ОРО; РОО;
    ОРР; РРО; РОР;
    РРР.

Эти комбинации равновероятны.

Видно, что вероятность того, что событие «Р» наступит k раз из N, равна произведению:

вероятности того, что k раз случилось событие «Р» – (p (Р))^k. В нашем случае p = 1/2;
вероятности того, что N – k раз случилось событие «не Р». В нашем случае это событие «О» – (p (О))^{N – k};
числу перестановок $C_{N}^{k} = \frac{N!}{k! (N - k)!} .$

Таким образом, $p_{k} (N) = C_{N}^{k} p^{k} {(1 - p)}^{N - k} .$

Распределение, описываемое формулой $p_{k} (N) = C_{N}^{k} p^{k} {(1 - p)}^{N - k},$ называется биномиальным.

Биномиальное распределение вероятности описывает процессы, в каждом из которых событие A может появиться с вероятностью p. Тогда вероятность того, что событие A наступит ровно k раз, определяется формулой $p_{k} (N) = C_{N}^{k} p^{k} {(1 - p)}^{N - k} .$

Математическое ожидание такого распределения легко посчитать из простых соображений. Поскольку результаты бросков кубика независимы, мы можем представить N бросков как N повторений одного броска. Напомним, что для N бросков $M_{k} = \sum_{i = 1}^{N} k_{i} p_{i},$ где $k_{i}$ – число успехов, а $p_{i}$ – вероятность того, что произойдет k успехов. Тогда математическое ожидание и дисперсия суммы испытаний равны сумме математических ожиданий и дисперсий одиночных событий: M = N p, D = N p (1 – p).

Биномиальное распределение при различных параметрах

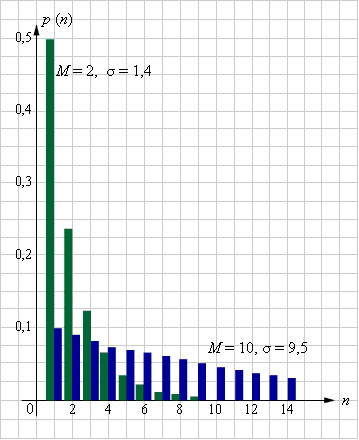
Сосуд с N молекулами идеального газа мысленно разделён на две части, V₁ и V₂. Найти вероятность того, что в объёме V₁ будет содержаться N₁, а в объёме V₂ будет содержаться N₂ молекул.

Имеем дело с биномиальным распределением с параметрами N = N₁ + N₂, n = N₁, $p = \frac{V_{1}}{V_{1} + V_{2}} .$ Таким образом, искомая вероятность равна $p_{N_{1}} (N_{1} + N_{2}) = C_{N}^{k} p^{k} {(1 - p)}^{N - k} = C_{N_{1} + N_{2}}^{N_{1}} {(\frac{V_{1}}{V_{1} + V_{2}})}^{N_{1}} {(\frac{V_{2}}{V_{1} + V_{2}})}^{N_{2}} .$

В частности, если объёмы частей сосуда равны друг другу, то вероятность обнаружить в половине сосуда ровно $N_{1}$ молекул описывается биномиальным распределением с математическим ожиданием $M_{x} = \frac{N}{2}$ и среднеквадратичным отклонением $σ = \frac{\sqrt{N}}{2} .$

Из пункта A по сети дорог идёт группа из N человек. На каждом перекрёстке, начиная с A, пришедшие туда люди с равной вероятностью поворачивают в направлении l и в направлении m. Сколько человек придёт в пункты B, C, D, …, I соответственно?

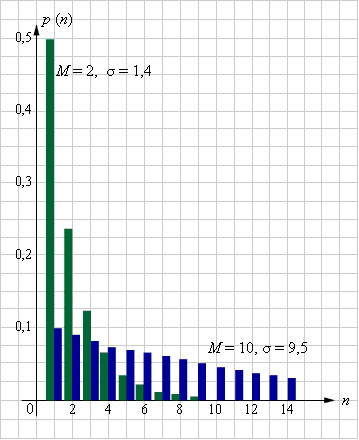
Допустим, что каждый человек уже повернул n раз. Все люди, вышедшие из пункта A, оказались в n-й строке. Обозначим число людей в каждой группе $\frac{x_{k, n}}{2^{n}},$ где k – номер группы, если их считать слева (см. рис. 4.3.6.3).

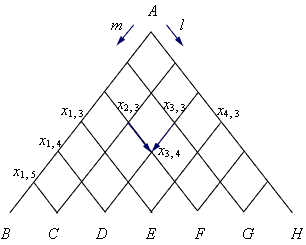
Заметим, что в пункт (k, n) пришла примерно половина от числа людей из пунктов (k, n – 1) и (k – 1, n – 1), или: $x_{k, n + 1} = x_{k - 1, n} + x_{k, n} .$ Выписав $x_{k, n}$ на соответствующих перекрёстках, мы получим треугольник Паскаля, коэффициенты которого равны $C_{n}^{k} .$ Значит, распределение вероятностей в k-й группе n-й строки – биномиальное c p = 0,5: $p_{k} (n) = C_{n}^{k} \frac{1}{2^{n}} .$ В нашем случае n = 6, и вероятность того, что человек окажется в k-м пункте, считая слева, равна $p_{k} = \frac{C_{6}^{k}}{2^{6}} .$

Если бы люди поворачивали вправо или влево с разной вероятностью, например, направо с вероятностью r, а налево – с вероятностью l = 1 – r, то распределение выглядело бы так: $p_{k, n} = C_{n}^{k} {(r)}^{n - k} {(1 - r)}^{k} .$

Биномиальное распределение связано с задачами о случайных блужданиях и перемешиваниях.

Пьяница случайным образом делает шаг вперёд или назад. Оцените, за какое количество шагов ему удастся добраться до дома, находящегося на расстоянии l от начала пути, при длине шага d?

Математическое ожидание положения человека в этой задаче равно нулю. Попасть домой человек сможет только случайно: если отклонится от начальной точки слишком далеко – как раз на расстояние до дома. Поэтому нам нужно найти не распределение вероятностей, а, фактически, среднеквадратичное отклонение длины пройденного пути за n шагов.

Перемещения за n и n + 1 шагов связаны соотношением L_{n + 1} = L_n ± d.

Возведём эту величину в квадрат и усредним: $\bar{L_{n + 1}^{2}} = \bar{L_{n}^{2}} \pm \bar{2 L_{n} d} + \bar{d^{2}} .$

Последний член просто равен математическому ожиданию, то есть нулю: $\bar{2 L_{n} d} = 2 {\bar{L}}_{n} d = 0,$ а $\bar{d^{2}} = d^{2}$ (величина d не является случайной). Тогда

\bar{L_{n + 1}^{2}} = \bar{L_{n}^{2}} + d^{2} .

Это формула арифметической прогрессии, значит,

\bar{L_{n}^{2}} = n d^{2} .

Отсюда средний пройденный за n шагов путь

\bar{L} = \sqrt{\bar{L_{n}^{2}}} = \sqrt{n} d .

Как уже было сказано выше, $\bar{L} = l,$ откуда $n = {(\frac{l}{d})}^{2} .$

Видно, что для того, чтобы преодолеть расстояние в 10 шагов, несчастному придётся сделать 100 шагов. Если до дома 100 шагов, то придётся прошагать целых 10000 раз.

Задача о пьянице, в свою очередь, отсылает нас к важному классу задач о диффузии и случайному перемешиванию сыпучих тел. Для каждого реального процесса распределение вероятностей выводится отдельно, но биномиальное распределение используется очень часто. Что будет, если увеличить количество испытаний N и шагать в одну сторону с очень маленькой вероятностью p, а в другую – с вероятностью, близкой к единице? Например, предположим, что Np → λ. При этих предположениях биномиальное распределение переходит в распределение Пуассона.

3. Распределение Пуассона имеет следующую плотность вероятности:

p_{k} (λ) = \frac{λ^{k}}{k!} e^{- λ} .

Биномиальное распределение описывается формулой $P = C_{N}^{k} p^{k} {(1 - p)}^{N - k} .$ Введём величину $λ = p N .$ Тогда $P = \frac{N (N - 1) ... (N - k + 1)}{k!} \frac{λ^{k}}{N^{k}} {(1 - \frac{λ}{N})}^{(N - k) (\frac{N}{λ} \frac{λ}{N})} = [1 ċ (1 - \frac{1}{N}) ċ ... ċ (1 - \frac{k - 1}{N})] \frac{λ^{k}}{k!} {[{(1 - \frac{λ}{N})}^{\frac{N}{λ}}]}^{λ (1 - \frac{k}{N})} .$ Перейдём в этой формуле к пределу при N → ∞. Первая квадратная скобка при этом будет стремиться к 1 (так как каждый её множитель стремится к 1), а вторая – к e^–1, что следует из определения замечательного предела e. Наконец, последняя скобка (в показателе степени) тоже будет стремиться к единице. Таким образом, $P = \frac{λ^{k}}{k!} e^{- λ} .$

Величина p_k (λ) соответствует вероятности ровно k удачных исходов при условии, что среднее число удачных исходов составляет λ.

Этим распределением проще пользоваться, чем биномиальным. Параметр λ (напомним, что он определяется пределом Np → λ) здесь равен числу, которое соответствует математическому ожиданию величины x: Mx = λ, Dx = λ.

Распределение Пуассона при различных λ и n

Закон Пуассона $p_{k} (λ) = \frac{λ^{k}}{k!} e^{- λ}$ действует всякий раз, когда имеется много независимых испытаний N, а вероятность p каждого испытания так мала, что среднее число событий λ = pN с данным исходом невелико.

В супе объёмом V плавает N перчинок. С какой вероятностью в ложку объёмом V₀ попадёт ровно n перчинок?

Если количество перчинок N велико, а отношение $\frac{V_{0}}{V}$ мало, то задача описывается распределением Пуассона.

В среднем, в ложке должны оказаться $λ = N \frac{V_{0}}{V}$ перчинок. Вероятность того, что в ложке окажется ровно n перчинок, равна $p_{n} (λ) = \frac{λ^{n}}{n!} e^{- λ} = \frac{{(N \frac{V_{0}}{V})}^{n}}{n!} e^{- N \frac{V_{0}}{V}} .$ В частности, при V = 10 л, $V_{0} = 0,01$ л, N = 50 получаем $λ \approx 0,05$ (то есть одна перчинка, в среднем, попадается на 20 ложек), а вероятность:

того, что в ложке окажется ноль перчинок, p₀ ≈ 0,95123,
того, что в ложке окажется одна перчинка, p₁ ≈ 0,04756,
того, что в ложке окажется две перчинки, p₂ ≈ 0,00119,
того, что в ложке окажется три перчинки, p₃ ≈ 0,00002.

Как видим, p_n очень быстро уменьшается с ростом n.

Распределением Пуассона описываются процессы типа количества телефонных вызовов за время t, вероятности аварий, оно же используется в теории страхования.

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Дискретные распределения вероятностей

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ